前言
mini-Vue 是精简版本的 Vue3,包含了 vue3 源码中的核心内容,附加上 demo 的具体实现。
本篇是最长上升子序列 篇,是关于 Vue3 中 LIS 的深入讨论。

LIS
Longest Increasing Subsequence 最长上升子序列。是指一个序列中最长的单调递增的子序列。
我们可以拿 leetcode 的题作为例子来编写:最长递增子序列

dp O(n²)
例子:
nums=[10,9,2,5,3,7,101,18]
dp 的思路如下:
初始化 dp 为 1 dp=[1,1,1,1,1,1,1,1],然后循环比对前面的,只要它大于了前面的数就把下标置为前面的数的最大长度+1,当然这个过程还要比较和自身的大小,如果自身更大取自身.最后返回最大值
过程
1
2
| 10 9 2 5 3 7 101 18
1 1 1 2 2 3 4 4
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| var lengthOfLIS = function (nums) {
let dp = new Array(nums.length).fill(1);
let max = 1;
for (let i = 0; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
max = Math.max(dp[i], max);
}
return max;
};
|
贪心 O(n²)
这个算法的核心是看最大的数然后更新
例子:
nums=[10,9,2,5,3,7,101,18,1]
过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| 10 9 2 5 101 3 7 18 1
init
arr 10
9<10 replace
arr 9
2<9 replace
arr 2
5>2 add
arr 2 5
101>5 add
arr 2 5 101
3<101 but 3>2 3<5(find first num bigger than this) replace
arr 2 3 101
7<101 replace
arr 2 3 7
18>7 add
arr 2 3 7 18
1<18 but 1<2 replace
arr 1 3 7 18
answer:4
|
所以我们可以知道,当他小于目标数组 arr 中末尾的数字的时候从头判断找到第一个比他大的数字执行替换的操作,大于的时候执行新增操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| var lengthOfLIS = function (nums) {
let arr = [nums[0]];
for (let i = 1; i < nums.length; i++) {
if (nums[i] <= arr[arr.length - 1]) {
for (let j = 0; j < arr.length; j++) {
if (nums[i] <= arr[j]) {
arr[j] = nums[i];
break;
}
}
} else {
arr.push(nums[i]);
}
}
return arr.length;
};
|
贪心+二分 O(nlogn)
我们可以发现,在查找的过程中该数组是一个有序数组,所以我们可以用二分查找进行优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| var lengthOfLIS = function (nums) {
let arr = [nums[0]];
for (let i = 1; i < nums.length; i++) {
if (nums[i] <= arr[arr.length - 1]) {
let l = 0,
r = arr.length - 1;
while (l <= r) {
let mid = ~~((l + r) / 2);
if (nums[i] > arr[mid]) {
l = mid + 1;
} else if (nums[i] < arr[mid]) {
r = mid - 1;
} else {
l = mid;
break;
}
}
arr[l] = nums[i];
} else {
arr.push(nums[i]);
}
}
return arr.length;
};
|
position 形成 LIS 的集合
我们真正需要做的实际上是生成一个带有原数据中对应下标的 LIS 的 seq 数组,而不是长度。所以我们应该先找到这一部分的 LIS,但为了找到这一部分的 LIS,我们又需要查看全部的元素的位置是否满足 LIS,举例
1
2
3
4
| num 10 9 2 5 101 3 7 18 1
pos 0 0 0 1 2 1 2 3 0
ans 2 3 7 18
|
如果我们有这么一个 pos 数组告诉我们具体的 LIS 下标,我们是不是就能很轻易得到对应的 LIS 元素了。
所以以这个出发去编写 pos 数组,它的过程如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| num 10 9 2 5 101 3 7 18 1
init
arr 10
pos 0
9<10 replace 10.index
arr 9
pos 0 0
2<9 replace 9.index
arr 2
pos 0 0 0
5>2 add len-1
arr 2 5
pos 0 0 0 1
101>5 add len-1
arr 2 5 101
pos 0 0 0 1 2
3<101 but 3>2 3<5(find first num bigger than this) replace && 5.index
arr 2 3 101
pos 0 0 0 1 2 1
7<101 replace 101.index
arr 2 3 7
pos 0 0 0 1 2 1 2
18>7 add len-1
arr 2 3 7 18
pos 0 0 0 1 2 1 2 3
1<18 but 1<2 replace 2.index
arr 1 3 7 18
pos 0 0 0 1 2 1 2 3 0
num 10 9 2 5 101 3 7 18 1
idx 0 1 2 3 4 5 6 7 8
pos 0 0 0 1 2 1 2 3 0
ans 2 3 7 18
idx 2 5 6 7
answerIdx:[2,5,6,7]
|
所以我们需要做的是,在每次 arr 进行 add 操作的时候,pos 就把 arr 的长度-1 放进来;在每次执行 replace 操作的时候,把二分查找替换的 l 传进来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| var lengthOfLIS = function (nums) {
const arr = [nums[0]];
const pos = [0];
for (let i = 1; i < nums.length; i++) {
if (nums[i] <= arr[arr.length - 1]) {
let l = 0,
r = arr.length - 1;
while (l <= r) {
let mid = ~~((l + r) / 2);
if (nums[i] > arr[mid]) {
l = mid + 1;
} else if (nums[i] < arr[mid]) {
r = mid - 1;
} else {
l = mid;
break;
}
}
arr[l] = nums[i];
pos.push(l);
} else {
arr.push(nums[i]);
pos.push(arr.length - 1);
}
}
return pos;
};
|
不过我们在操作到这里的时候,只是得到了一个下标集合,刚才的 answerIdx 是我们自己判断出来的,接下来我们就实现 answerIdx 这一步
cur 得到 seq
answerIdx 这一步,是将 pos 中的 LIS 转为了对应的 idx。我们仔细观察可以发现,其实 pos 的长度是和 idx 一样的,因为它就是全部元素形成 LIS 的一个集合,而我们又发现也得到 arr 了,arr 的长度-1 就是 pos 中最大的元素,所以我们不妨设置一个变量 cur,让他等于 arr 的最大长度-1,此时我们只要从后往前遍历 pos,当 cur 和 pos 的数据是一样的时候,就说明这个数据是不用移动的,就可以把 pos 中对应的下标加入到 seq 数组中。然后又因为我们这个 arr 其实是不会再用到的了,所以可以直接复用 arr。下面来演示这个过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| num 10 9 2 5 101 3 7 18 1
num 10 9 2 5 101 3 7 18 1
idx 0 1 2 3 4 5 6 7 8
arr 1 3 7 18
pos 0 0 0 1 2 1 2 3 0
cur 3
pos 0
pos 3 cur-- arr[1,3,7,7]
pos 2 cur-- arr[1,3,6,7]
pos 1 cur-- arr[1,5,6,7]
...
pos 0 cur-- arr[2,5,6,7]
cur=-1 stop
arr: [2,5,6,7]
answer:[2,3,7,18]
|
这样就获得了这个 seq 数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| var lengthOfLIS = function (nums) {
const arr = [nums[0]];
const pos = [0];
for (let i = 1; i < nums.length; i++) {
if (nums[i] <= arr[arr.length - 1]) {
let l = 0,
r = arr.length - 1;
while (l <= r) {
let mid = ~~((l + r) / 2);
if (nums[i] > arr[mid]) {
l = mid + 1;
} else if (nums[i] < arr[mid]) {
r = mid - 1;
} else {
l = mid;
break;
}
}
arr[l] = nums[i];
pos.push(l);
} else {
arr.push(nums[i]);
pos.push(arr.length - 1);
}
}
let cur = arr.length - 1;
for (let i = pos.length - 1; i >= 0 && cur >= 0; i--) {
if (cur === pos[i]) {
arr[cur--] = i;
}
}
return arr;
};
|
source
我们之前说过 source 为-1 的时候是直接更新,所以我们也应该在算法里面移除-1 的考虑
最后全部代码为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function getSequence(nums) {
const arr = [nums[0]];
const pos = [0];
for (let i = 1; i < nums.length; i++) {
if (nums[i] === -1) continue;
if (nums[i] <= arr[arr.length - 1]) {
let l = 0,
r = arr.length - 1;
while (l <= r) {
let mid = ~~((l + r) / 2);
if (nums[i] > arr[mid]) {
l = mid + 1;
} else if (nums[i] < arr[mid]) {
r = mid - 1;
} else {
l = mid;
break;
}
}
arr[l] = nums[i];
pos.push(l);
} else {
arr.push(nums[i]);
pos.push(arr.length - 1);
}
}
let cur = arr.length - 1;
for (let i = pos.length - 1; i >= 0 && cur >= 0; i--) {
if (cur === pos[i]) {
arr[cur--] = i;
}
}
return arr;
}
|
key
最后回到本源,我们要给 vnode 添加一个 key 属性
1
2
3
4
5
6
7
8
9
| return {
type,
props,
children,
shapeFlag,
el: null,
anchor: null,
key: props && props.key,
};
|
另外在 patchProps 里面也要注意 key 的判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
for (const key in oldProps) {
if (key === "key") {
continue;
}
if (newProps[key] == null) {
patchDomProp(oldProps[key], null, key, el);
}
}
for (const key in newProps) {
if (key === "key") {
continue;
}
if (oldProps[key] !== newProps[key]) {
patchDomProp(oldProps[key], newProps[key], key, el);
}
}
|
总结
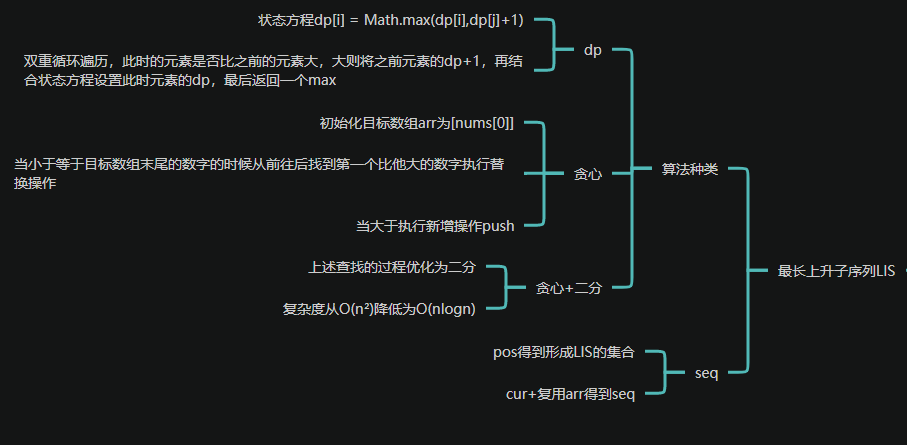
在本节中我们以 leetcode 为例学习了 LIS 算法的核心原理,使用 dp,贪心去实现,然后又通过二分优化了查找过程,后面我们发现我们需要的是实际的元素而不是下标,就采用了 pos 数组帮助我们得到了形成 LIS 的集合,再设置 cur 并复用 arr 得到我们的 seq 数组。下节我们将介绍组件。