前言

在上一篇笔记里面，我们深入了解了前序和后序遍历的本质，学会了翻转二叉树，将二叉树转为链表和填充二叉树右侧指针三道问题。接下来进一步学习，在本篇能理解并运用以下题目：

Leetcode
654.最大二叉树
 105.从前序遍历和中序遍历构造二叉树
 106.从中序和后序遍历构造二叉树
 889.根据前序和后序遍历构造二叉树

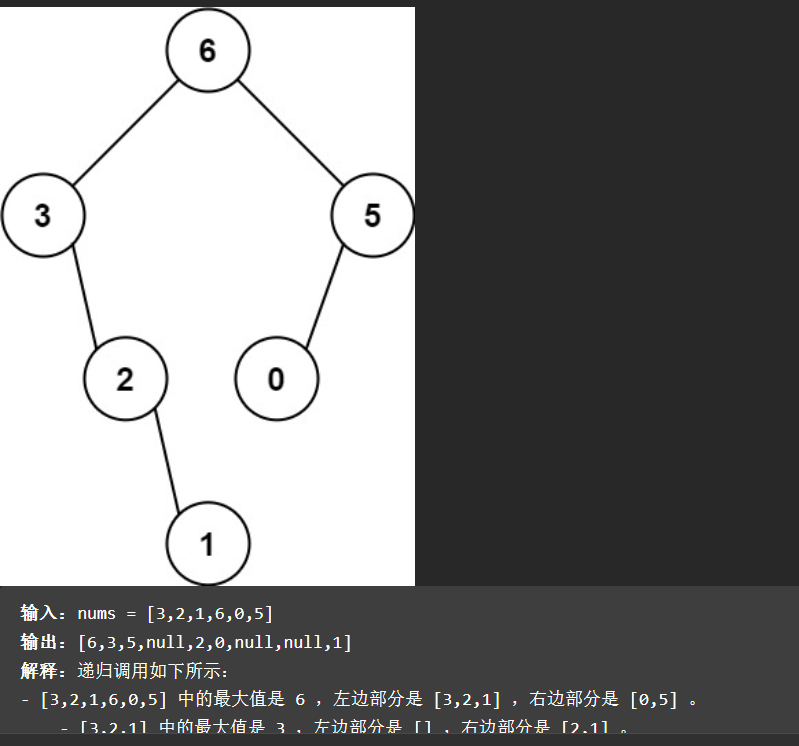
最大二叉树

我们细分这道题，其实他在做这样的事情

var constructMaximumBinaryTree = function ([3,2,1,6,0,5]) {
    // 找到数组的最大值
    const root = new TreeNode(6)
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

再详细一点就是如下的思路：

var constructMaximumBinaryTree = function (nums) {
    let len = nums.length-1;
    const build = (nums,start,end)=>{
        if(start>end)return null;
        //查找最大值和他的下标
        let max = -Infinity,index;
        for(let i=start;i<=end;i++){
            if(nums[i]>max){
                max = nums[i];
                index = i;
            }
        }
        //构造二叉树
        const root = new TreeNode(max);
        root.left = build(nums,start,index-1);
        root.right = build(nums,index+1,end);
        return root;
    }
    return build(nums,0,len);
};
// 或者可以这样
var constructMaximumBinaryTree = function (nums) {
    //查找最大值和他的下标
    if(!nums.length)return null;
    let max = -Infinity, index = -1;
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] > max) {
            max = nums[i];
            index = i;
        }
    }
    //构造二叉树
    const root = new TreeNode(max);
    root.left = constructMaximumBinaryTree(nums.slice(0, index));
    //+1
    root.right = constructMaximumBinaryTree(nums.slice(index + 1));
    return root;
};

至此第一道构造二叉树的题目就做完了，接下看看另外两道题目

通过前序和中序遍历结果构造二叉树

我们知道前序遍历的第一个节点就是整个树的根，那么中序遍历的根节点前面就是左子树，后面就是右子树，利用这个特性，自然而然的会想出以下代码

const build = (preorder, inorder)=>{
    //找到根节点
    const root = preorder.shift();
    // 中序找到该节点的下标
    const rootIndex = inorder.indexOf(root);
    const tree = new TreeNode(root);
    //递归调用构造左右子树
    tree.left = fun(...);
    tree.right = fun(...);
    return tree;
}

那么问题来了，我们这里要创建一个什么样的函数去递归呢？
其实我们只要利用我们的中序数组就可以了，因为能依靠他查找，就能依靠他构造

var buildTree = function(preorder, inorder) {
    const build = (inorder)=>{
        if(!inorder||!inorder.length)return null;
        const root = preorder.shift();
        const rootIndex = inorder.indexOf(root);
        const tree = new TreeNode(root);
        tree.left = build(inorder.slice(0,rootIndex));
        tree.right = build(inorder.slice(rootIndex+1));
        return tree;
    }
    return build(inorder);
};

或者我们可以这样,我们知道了其实前序的左子树终止边界就是中序到根节点的长度+1，那么我们也就可以带入前序递归

var buildTree = function(preorder, inorder) {
    if (!preorder.length) return null
    const root = preorder.shift();
    const tree = new TreeNode(root)
    const rootIndex = inorder.indexOf(root)
    tree.left = buildTree(preorder.slice(0, rootIndex), inorder.slice(0,rootIndex))
    tree.right = buildTree(preorder.slice(rootIndex), inorder.slice(rootIndex+1))
    return tree
};

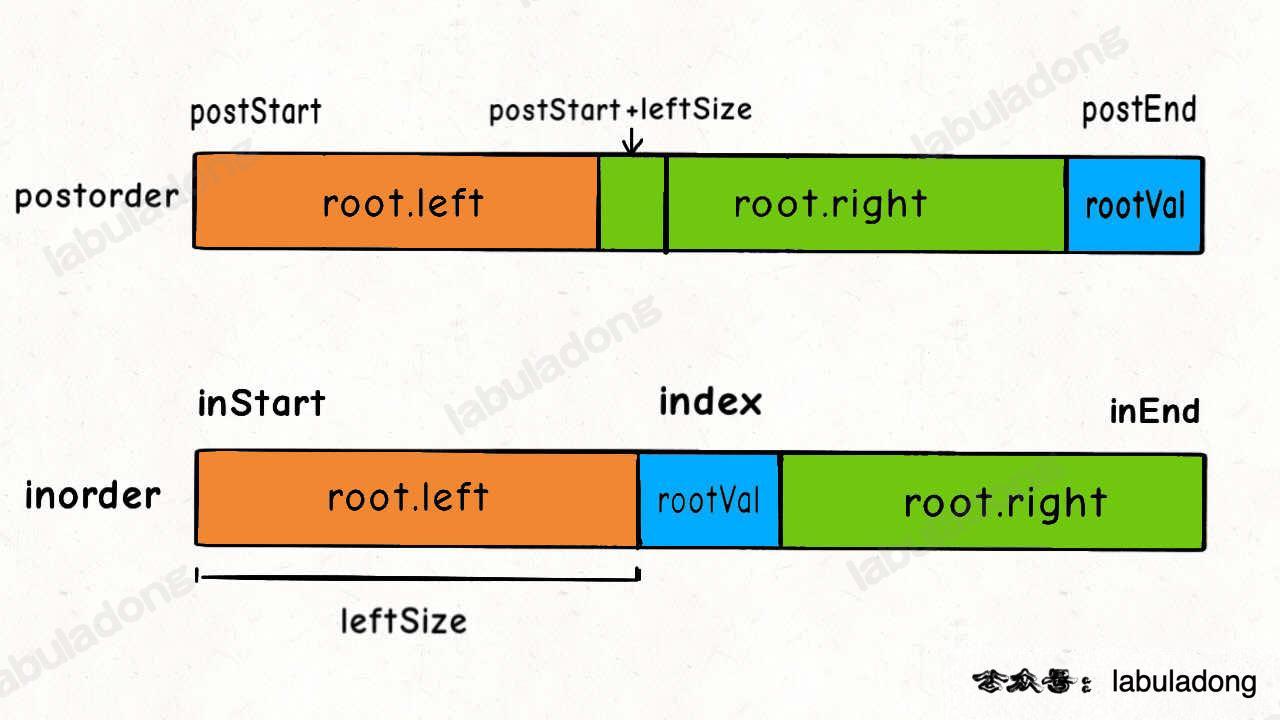
通过后序和中序遍历结果构造二叉树

后序遍历的最后一个节点是root，那么我们知道了这个道理，其实就把shift的操作变成pop即可。

var buildTree = function(inorder, postorder) {
    if(!postorder.length)return null;
    const root = postorder.pop();
    const rootIndex = inorder.indexOf(root);
    const tree = new TreeNode(root);
    tree.left = buildTree(inorder.slice(0,rootIndex),postorder.slice(0,rootIndex));
    tree.right = buildTree(inorder.slice(rootIndex+1),postorder.slice(rootIndex));
    return tree
};

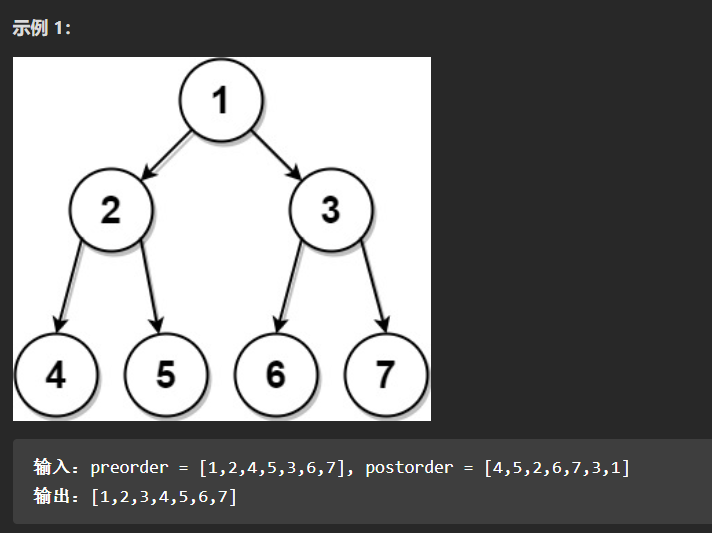
通过前序和后序构造二叉树

我们知道了结合中序构造的方法，就是从中序中找到对应的index然后分离左右，最后递归。

那么前序和后序怎么构造呢？

实际上，拿前序当参照物，第一个就是根节点，第二个就是左子树的根节点，那么我们就可以同样的在后序中找到这个左子树根节点，去分离我们的左右子树。

var constructFromPrePost = function(preorder, postorder) {
    if(!preorder.length||!postorder.length)return null;
    if(preorder.length===1)return new TreeNode(preorder[0]);
    const root = preorder[1];
    const index = postorder.indexOf(root);
    const tree = new TreeNode(preorder.shift());
    //之前找的是根节点前面的一段，所以是index，现在找的是左子树根节点，所以index+1
    tree.left = constructFromPrePost(preorder.slice(0,index+1),postorder.slice(0,index+1),)
    tree.right = constructFromPrePost(preorder.slice(index+1),postorder.slice(index+1))
    return tree;
};