前言
mini-Vue 是精简版本的 Vue3,包含了 vue3 源码中的核心内容,附加上 demo 的具体实现。
本篇是核心 diff 篇,是关于 Vue3 中 patch 的深入讨论。

patchArrayChildren 的问题
在上一节我们实现了patchArrayChildren,但是我们这个实现是比较简单粗暴的,直接对数组一对一进行的 diff 操作。
实际上它还是存在一些问题的,看下面的例子
c1: a b c
c2: x a b c
我们在新孩子头部插入了一个节点,很明显我们只要在 a 前面插入一个 x 即可。但是按照我们现在的做法,它需要每个都变化一次。
所以有没有办法解决这个问题?有的,就是要引入一个 key 去告诉框架什么节点是应该去复用的,从而减小操作虚拟 DOM 的次数
而我们前面实现的 patchArrayChildren 其实就是 patchUnkeyedChildren
这里先偷个懒 只要第一个元素有 key 就当作有 key
1
2
3
4
5
6
7
8
| if (prevShapeFlag & ShapeFlags.ARRAY_CHILDREN) {
if (c1[0] && c1[0].key != null && c2[0] && c2[0].key != null) {
patchkeyedChildren(c1, c2, container, anchor);
} else {
patchUnkeyedChildren(c1, c2, container, anchor);
}
}
|
patchUnkeyedChildren

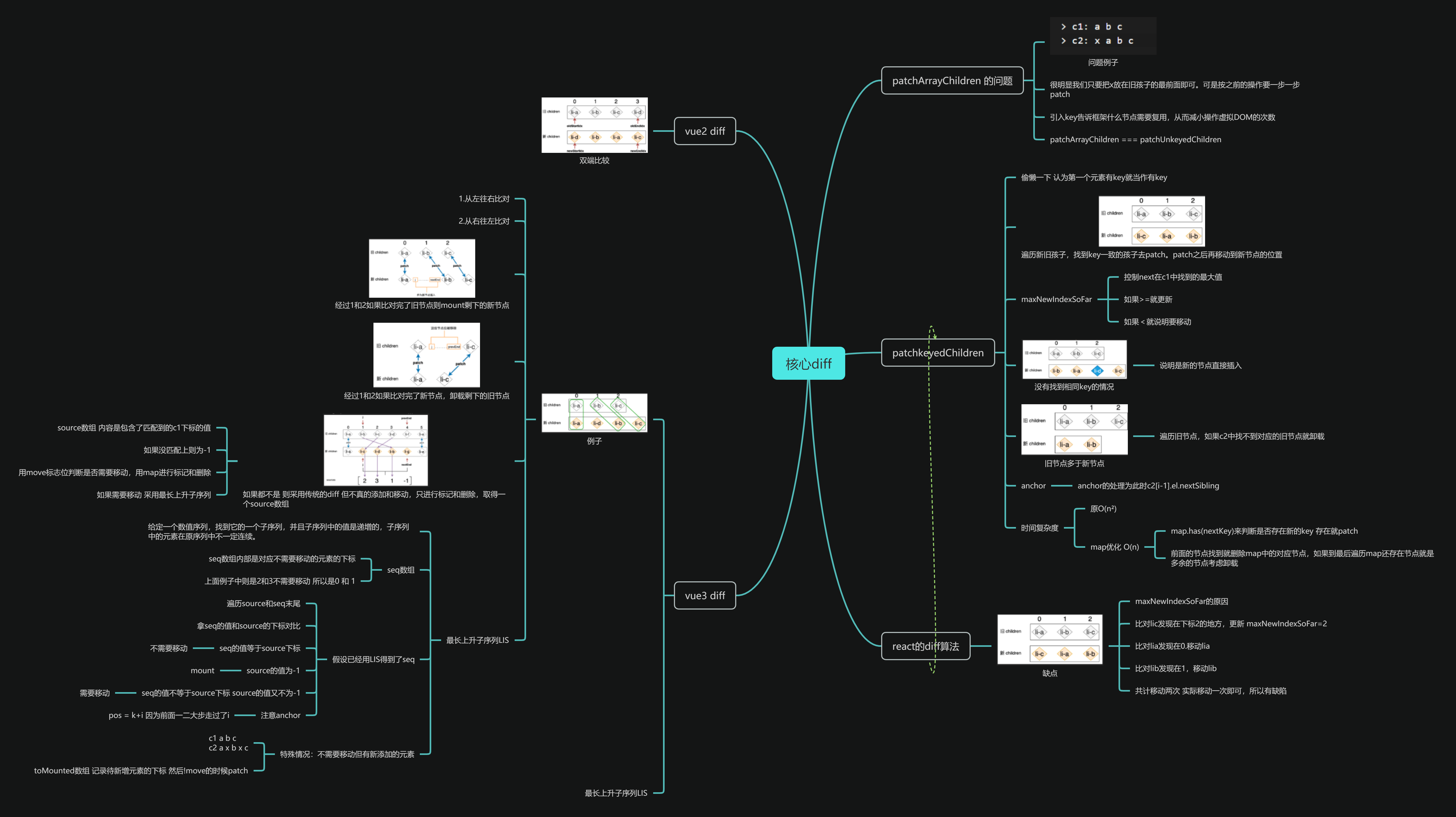
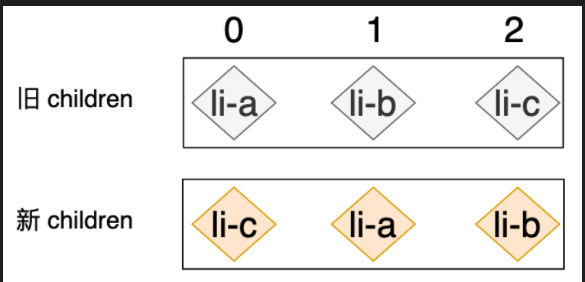
根据上面的图,我们先按最简单的方式去写 patchkeyedChildren,首先我们遍历新旧孩子,然后,找到 key 一致的新旧孩子去进行 patch。patch 之后再移动到新节点的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| function patchkeyedChildren(c1, c2, container, anchor) {
for (let i = 0; i < c2.length; i++) {
const next = c2[i];
for (let j = 0; j < c1.length; j++) {
const prev = c1[i];
if (next.key === prev.key) {
patch(prev, next, container, anchor);
const curAnchor = i === 0 ? c1[0].el : c2[i - 1].el.nextSibling;
container.insertBefore(next.el, curAnchor);
break;
}
}
}
}
|
maxNewIndexSoFar
进一步优化,因为上个版本不管顺序如何都会进行 insertBefore 操作.当他确实需要移动的时候我们才去移动
举例
1
2
3
4
5
6
7
| c1 > a b c
c2 > a c b
maxNewIndexSoFar = 0
a -- a c1 = 0 = 0 => maxNewIndexSoFar = 0
c -- c c1 = 2 > 0 => update maxNewIndexSoFar = 2
b -- b c1 = 1 < 2 => move b
|
我们需要设置一个变量来记录 next 在 c1 中找到的最大值,如果小于这个值则移动大于或等于则更新这个值.这样就做到了有需要移动的时候才移动.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function patchkeyedChildren(c1, c2, container, anchor) {
let maxNewIndexSoFar = 0;
for (let i = 0; i < c2.length; i++) {
const next = c2[i];
for (let j = 0; j < c1.length; j++) {
const prev = c1[i];
if (next.key === prev.key) {
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
const curAnchor = c2[i - 1].el.nextSibling;
container.insertBefore(next.el, curAnchor);
} else {
maxNewIndexSoFar = j;
}
break;
}
}
}
}
|
find 标志位
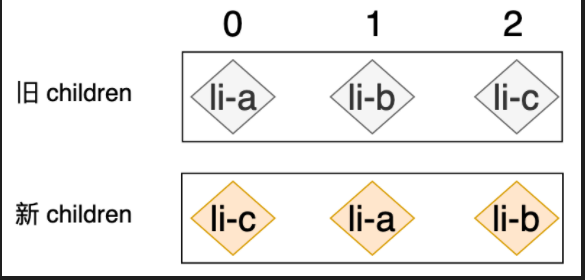
再考虑 c1 中没有找到相同 key 的情况

所以我们设置一个标志位,来决定是否存在这种情况,如果循环结束都没用改变状态则说明是新的节点,直接插入即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function patchkeyedChildren(c1, c2, container, anchor) {
let maxNewIndexSoFar = 0;
for (let i = 0; i < c2.length; i++) {
const next = c2[i];
let find = false;
for (let j = 0; j < c1.length; j++) {
const prev = c1[i];
if (next.key === prev.key) {
find = true;
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
const curAnchor = c2[i - 1].el.nextSibling;
container.insertBefore(next.el, curAnchor);
} else {
maxNewIndexSoFar = j;
}
break;
}
}
if (!find) {
const curAnchor = i === 0 ? c1[0].el : c2[i - 1].el.nextSibling;
patch(null, next, container, curAnchor);
}
}
}
|
旧节点多于新节点的时候
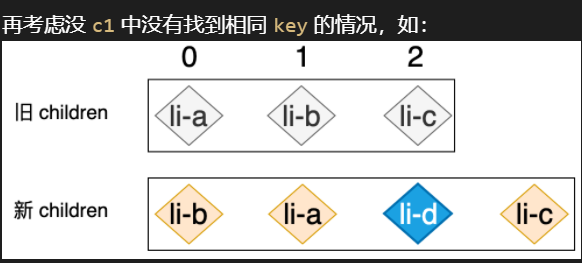
还有一种情况,就是旧节点多于新节点的时候

这时候我们就要移除多余的旧节点,遍历旧节点如果 c2 中找不到此节点就卸载
1
2
3
4
5
6
7
|
for (let i = 0; i < c1.length; i++) {
const prev = c1[i];
if (!c2.find((next) => next.key === prev.key)) {
unmount(prev);
}
}
|
map 优化
此时我们的算法复杂度是 O(n²),我们可以拿 map 来优化一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| const map = new Map();
c1.forEach((prev, j) => {
map.set(prev.key, {
prev,
j,
});
});
let maxNewIndexSoFar = 0;
for (let i = 0; i < c2.length; i++) {
const next = c2[i];
if (map.has(next.key)) {
const { prev, j } = map.get(next.key);
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
const curAnchor = c2[i - 1].el.nextSibling;
container.insertBefore(next.el, curAnchor);
} else {
maxNewIndexSoFar = j;
}
} else {
const curAnchor = i === 0 ? c1[0].el : c2[i - 1].el.nextSibling;
patch(null, next, container, curAnchor);
}
}
|
对于我们最后的旧节点多余的情况的优化,可以采用这样的思路,如果前面的节点找到就删除,一直到最后,如果还有存在的节点,就是多余的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| if (map.has(next.key)) {
const { prev, j } = map.get(next.key);
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
const curAnchor = c2[i - 1].el.nextSibling;
container.insertBefore(next.el, curAnchor);
} else {
maxNewIndexSoFar = j;
}
map.delete(next.key);
}
...
map.forEach(({prev}) => {
unmount(prev);
});
|
至此算法复杂度就降低到了 O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function patchkeyedChildren(c1, c2, container, anchor) {
const map = new Map();
c1.forEach((prev, j) => {
map.set(prev.key, {
prev,
j,
});
});
let maxNewIndexSoFar = 0;
for (let i = 0; i < c2.length; i++) {
const next = c2[i];
const curAnchor = i === 0 ? c1[0].el : c2[i - 1].el.nextSibling;
if (map.has(next.key)) {
const { prev, j } = map.get(next.key);
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
container.insertBefore(next.el, curAnchor);
} else {
maxNewIndexSoFar = j;
}
map.delete(next.key);
} else {
patch(null, next, container, curAnchor);
}
}
map.forEach(({ prev }) => {
unmount(prev);
});
}
|
据说以上的 diff 算法就是 react 的 diff 算法
缺点
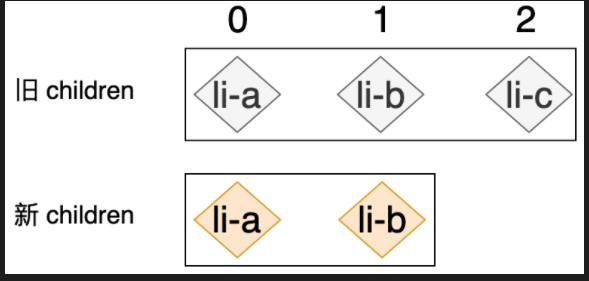
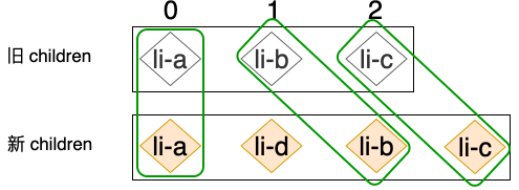
对于此算法来说,有一个缺点:

这个情况肉眼可见只需要移动一次 li-c 节点即可.但实际上,react 的 diff 算法移动了两次
原因是:首先比较 li-c 发现旧节点下标 2 的地方就是 li-c,于是刷新 maxNewIndexSoFar 为 2,接着 li-a 开始找,找到下标 0,0 小于 2,此时需要交换 li-a,li-b 开始找,找到下标 1,1 小于 2,也需要交换,所以这里有缺点.
vue2 diff
为了解决这个问题,vue2 采用了双端比较的方法,来对四个端点进行比较和移动,如果都不行再逐个比较.

vue3 diff
在 Vue3 中将采用另外一种核心 Diff 算法,它借鉴于 ivi 和 inferno
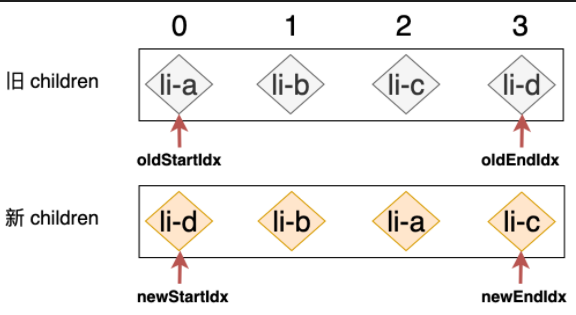
从左往右再从右往左
首先从左往右依次比对 然后从右往左依次比对

1
2
3
4
5
6
7
8
9
10
11
12
13
14
| let i = 0;
let e1 = c1.length - 1;
let e2 = c2.length - 1;
while (i <= e1 && i <= e2 && c1[i].key === c2[i].key) {
patch(c1[i], c2[i], container, anchor);
i++;
}
while (i <= e1 && i <= e2 && c1[e1].key === c2[e2].key) {
patch(c1[e1], c2[e2], container, anchor);
e1--;
e2--;
}
|
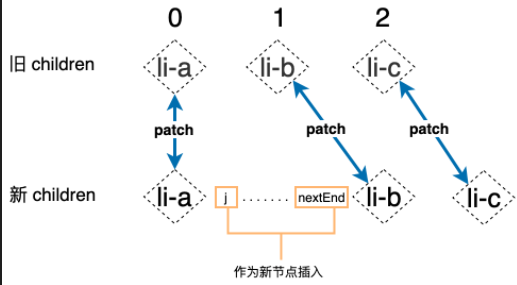
对比完的情况一
经过上述操作如果将旧节点比对完,则 mount 剩下的新节点 此时 i>e1

1
2
3
4
5
6
7
8
9
10
11
12
| if (i > e1) {
for (let j = i; j <= e2; j++) {
const nextPos = e2 + 1;
const curAnchor = (c2[nextPos] && c2[nextPos].el) || anchor;
patch(null, c2[j], container, curAnchor);
}
}
|
对比完的情况二
经过上述操作如果将新节点对比完,则 unmount 剩下的旧节点 此时 i>e2

1
2
3
4
5
6
| else if (i > e2) {
for (let j = i; j <= e1; j++) {
unmount(c1[j]);
}
}
|
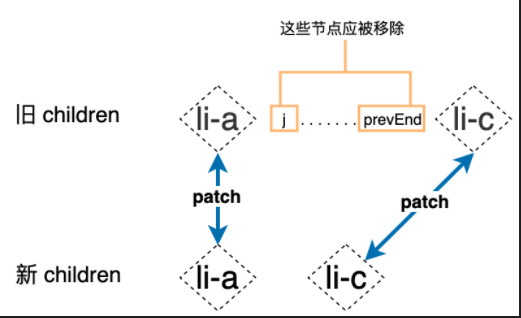
不满足则采用传统 diff(标记和删除)
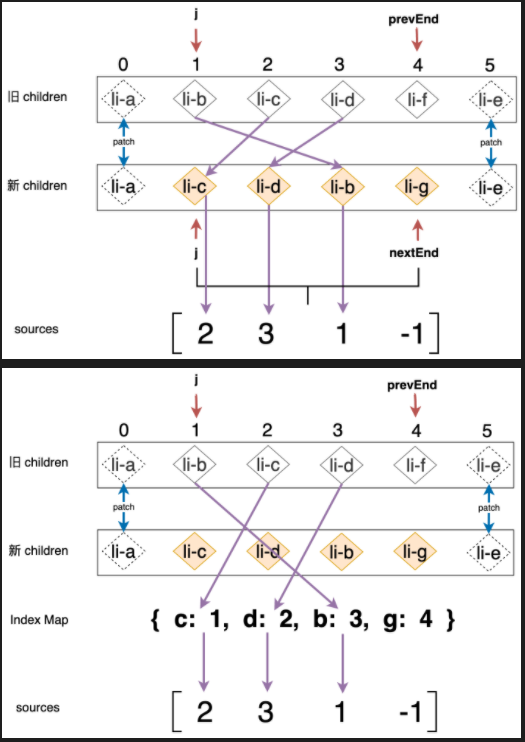
若不满足以上的情况,则采用传统的 diff 算法,但不真的添加和移动,只进行标记和删除 取得一个 source 数组,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| else {
const map = new Map();
for (let j = i; j <= e1; j++) {
const prev = c1[j];
map.set(prev.key, {
prev,
j
});
}
let maxNewIndexSoFar = 0;
let move = false;
const source = new Array(e2-i+1).fill(-1);
for (let k = 0; k < source.length; k++) {
const next = c2[k+i];
if (map.has(next.key)) {
const {
prev,
j
} = map.get(next.key);
patch(prev, next, container, anchor);
if (j < maxNewIndexSoFar) {
move = true;
} else {
maxNewIndexSoFar = j;
}
source[k] = j;
map.delete(next.key);
} else {
}
}
map.forEach(({
prev
}) => {
unmount(prev)
})
}
|
然后我们要编写 move 的情况了,需要移动的话,我们要采用最长上升子序列算法.
最长上升子序列
先说结论,最长上升子序列的节点不需要移动,用这个算法会得到 source 数组里面最长上升子序列的对应下标,合起来是一个 seq 数组,这个数组里面的元素不需要移动。
TIP
什么是最长递增子序列:给定一个数值序列,找到它的一个子序列,并且子序列中的值是递增的,子序列中的元素在原序列中不一定连续。
例如给定数值序列为:[ 0, 8, 4, 12 ]
那么它的最长递增子序列就是:[0, 8, 12]
当然答案可能有多种情况,例如:[0, 4, 12] 也是可以的
假设我们现在已经采取了最长上升子序列算法完成了 seq 数组,进行下一步的判断。
设两个指针都指向 source 和 seq 的末尾。
1
2
3
4
| const seq = getSequence(source);
let j = seq.length - 1;
for (let k = source.length - 1; k >= 0; k--) {}
|
不需要移动的情况
如果此时 seq 中的值和 source 的下标对应,说明不需要移动,两指针都减一进行下一轮比较
1
2
3
4
5
| if (seq[j] == k) {
j--;
}
|
需要 mount 的情况
如果此时 source 的值为-1,说明这个节点需要 mount,source 指针减一
1
2
3
4
| if (source[k] === -1) {
patch(null, c2[pos], container, curAnchor);
}
|
需要移动的情况
如果此时 source 的值不为-1 且它的下标又不和 seq 中的值对应,则需要移动,source 减一
1
2
3
4
| if (...) {
container.insertBefore(c2[pos].el, curAnchor);
}
|
注意 anchor
那么现在的问题是这个 anchor 和 pos 要怎么写,对于 pos,因为此时我们是进行了前面说的一二大步骤才进入这个传统 diff 的,已经走了 i 步,所以起点要加 i。
对于 anchor 来说,它其实就是当前节点的下一位,当然还要考虑末尾的情况所以是:
1
2
| const nextPos = pos + 1;
const curAnchor = (c2[nextPos] && c2[nextPos].el) || anchor;
|
我们会发现上面有两种情况都需要 anchor 和 pos,所以我们可以合并一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| if (move) {
const seq = getSequence(source);
let j = seq.length - 1;
for (let k = source.length - 1; k >= 0; k--) {
if (seq[j] == k) {
j--;
} else {
const pos = k + i;
const nextPos = pos + 1;
const curAnchor = (c2[nextPos] && c2[nextPos].el) || anchor;
if (source[k] === -1) {
patch(null, c2[pos], container, curAnchor);
} else {
container.insertBefore(c2[pos].el, curAnchor);
}
}
}
}
|
特殊情况:不需要移动,但还有未添加的元素
c1: a b c
c2: a x b y c
source: [1,-1,2,-1,3]
seq: [1,2,3]
上面的例子,move 是 false,因此专门用一个 toMounted 去处理这种情况
toMounted 记录待新增的元素的下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| const toMounted = [];
...
if(...){
}else{
toMounted(k+i);
}
...
if(toMounted.length){
for(let k=toMounted.length-1;k>=0;k--){
const pos = toMounted[k];
const nextPos = pos+1;
const curAnchor = (c2[nextPos]&&c2[nextPos].el) || anchor;
patch(null,c2[pos],container,curAnchor);
}
}
|
总结
我们在这一节通过 patchArrayChildren 暴露出来的一对一对比低效的问题,找到了添加 key 去判断的解决方法,其中编写了 patchUnkeyedChildren 来对比新旧孩子,找到 key 一致的孩子去进行 patch,然后我们通过 maxNewIndexSoFar 去优化 insertBefore 的情况,让它在合适的时候才插入,再通过 find 标志位标志新节点没有找到旧节点的情况,直接 mount,随后再判断旧节点多于新节点的情况,直接卸载多余的旧节点。接着我们通过 map 优化了上述的循环代码,让复杂度从 O(n²)降低到 O(n).
当我们完成后又根据一个简单的例子(移动多次)发现该 diff 算法的缺点,随后看到了 vue2 vue3 解决该问题的方法。其中我们对 vue3 的 diff 算法进行深入了解。vue3 的 diff 是先从左往右对比再从右往左对比,找到需要 mount 的新节点区间或需要卸载的旧节点区间。找不到这两个情况就进行传统的 diff,不过不进行挂载和移动,还是用一个 map 进行标记和删除。之后对于先前 react 算法的缺点,用最长上升子序列解决。最长上升子序列的数组内的元素不需要移动。我们又判断了挂载(source 为-1)和移动(不为-1 又不和 seq 对上)的情况,来进行挂载和移动的操作。最后对于特殊的情况,就是旧节点间夹杂需要挂载的新节点的情况。去设置一个 toMounted 数组,在非 move 的情况时把对应的下标加入到数组中,后面单独拿出来挂载。
本节的遗漏的最长上升子序列算法将在下一节讲述。