前言

在前面的文章我们学习了BST二叉搜索树的性质，以及结合中序遍历的性质，可以实现树的升序和降序，以及累加树的操作。下面这篇文章深入讲解BST的性质，判断BST的合法性，增删改查，读完本文你对下面的算法题会有更深入的了解

Leetcode
450.删除二叉搜索树的节点
701.二叉搜索树中的插入操作
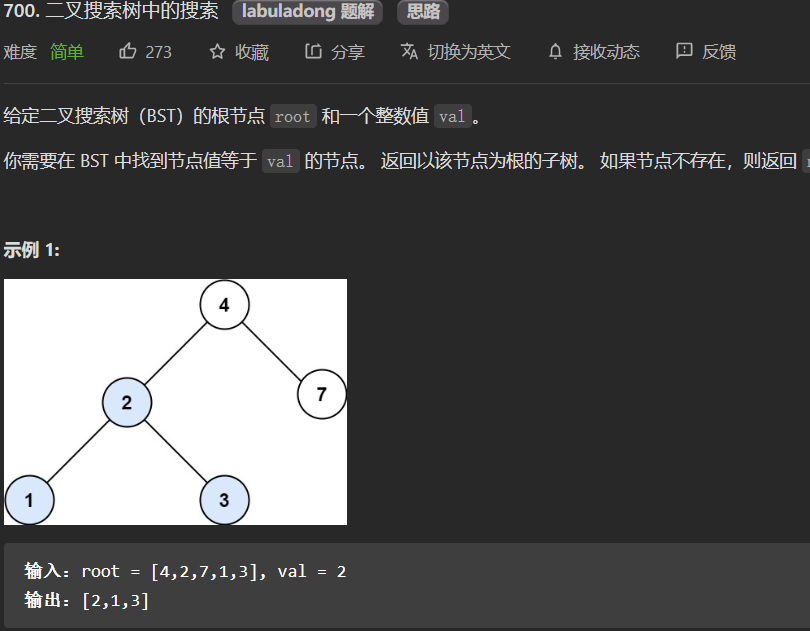
700.二叉搜索树中的搜索
98.验证二叉搜索树

BST简介

所谓的二叉搜索树，就是左小右大的二叉树。利用他的性质，我们可以做到类似二分搜索的操作，搜索一个元素的效率很高，

对于BST相关的问题，我们经常会看到以下代码逻辑

1
2
3
4
5
6
7
8
9
10
11
const BST = (root,target)=>{
    if(root.val===target){
        //do something...
    }
    if(root.val<target){
        BST(root.right,target);
    }
    if(root.val>target){
        BST(root.left,target);
    }
}

这个代码框架其实和二叉树遍历差不多，无非就是利用了BST左小右大的特性

下面来讲几道BST必会的题目

判断BST的合法性

这里存在了坑点，按照我们之前思考的二叉树节点应该做什么的做法，这里会写出以下的code

1
2
3
4
5
6
7
8
9
10
const judgeBST = n=>{
    if(!n)return true;
    if(n.left!==null&&n.val<n.left.val){
        return false;
    }
    if(n.right!==null&n.val>n.right.val){
        return false;
    }
    return judgeBST(n.left)&&judgeBST(n.right)
}

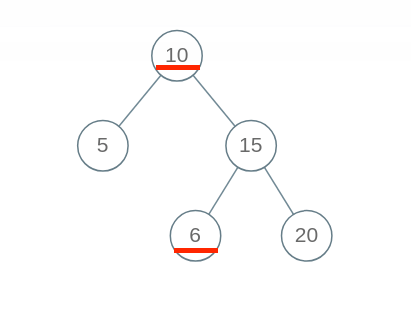
看似好像没什么问题，但是实际上这个算法出现了错误，原因在于BST的性质。对于这个算法来说，他判断的是每个节点的值要大于左边小于右边，但是BST的性质是对于每个节点，他的值都要小于右子树的全部值，大于左子树的全部值，看图：

该图不是BST，但是他会被这个算法判定为BST

那么我们应该怎么做呢？既然要满足当前节点大于左子树全部值，小于右子树全部值，我们不妨设个变量max和min，分别来代替左右子树的最大值，一旦没有满足这个条件就视为非BST

1
2
3
4
5
6
7
8
9
10
//如果满足max>root.val>min就正确
const isValidBST = (n,max,min)=>{
    if(!n)return true;
    //注意这里是判断子树不为空
    if(min!==null&&n.val<=min.val)return false;
    if(max!==null&&n.val>=max.val)return false;
    //对于左子树来说，最大值是n，对于右子树来说，最小值是n
    return isValidBST(n.left,n,min)&&isValidBST(n.right,max,n);
}
return isValidBST(root,null,null);

在BST中搜索元素

如果是一颗普通的二叉树可以写如下的代码

1
2
3
4
5
6
7
const searchBST = (n,target)=>{
    if(!n)return null;
    if(n.val === target) return n;
    let left = searchBST(n.left,target);
    let right = searchBST(n.right,target); 
    return left!==null?left:right
}

这段代码相当于穷举了二叉树中的所有节点，如果找的到就返回对应的子树.

但我们拥有BST的性质，就应该利用起来，比较root和target的值，将其中的一边舍去。

1
2
3
4
5
6
const searchBST = (n,target)=>{
    if(!n)return null;
    if(n.val<target)return searchBST(n.right,target);
    if(n.val>target)return searchBST(n.left,target);
    return n;
}

在BST中插入一个数

对于数据结构的操作无非就是遍历+访问，其中遍历就是找，访问就是改。具体而言，插入一个数据就首先要找到插入的位置，然后进行插入操作。

上一个问题，我们总结了BST的遍历框架，也就是找的问题，直接套框架，然后我们只要进行改的操作就可以了。但是要注意的是，一旦涉及到改，函数就要返回treenode类型，并且对递归调用的返回值进行接收

1
2
3
4
5
6
7
8
9
10
const insertIntoBST = function(root, val) {
    if(!root) return new TreeNode(val);
    if(root.val<val){
        root.right = insertIntoBST(root.right,val);
    }
    if(root.val>val){
        root.left = insertIntoBST(root.left,val);
    }
    return root;
}

在BST中删除一个数

这个问题比较复杂，但是思路也差不多，先找到再改，框架如下

1
2
3
4
5
6
7
8
9
10
var deleteNode = function(root, key) {
    if(root.val === key){
        //delete
    }else if(root.val<key){
        root.left = deleteNode(root.left,key);
    }else{
        root.right = deleteNode(root.right,key);
    }
    return root;
}

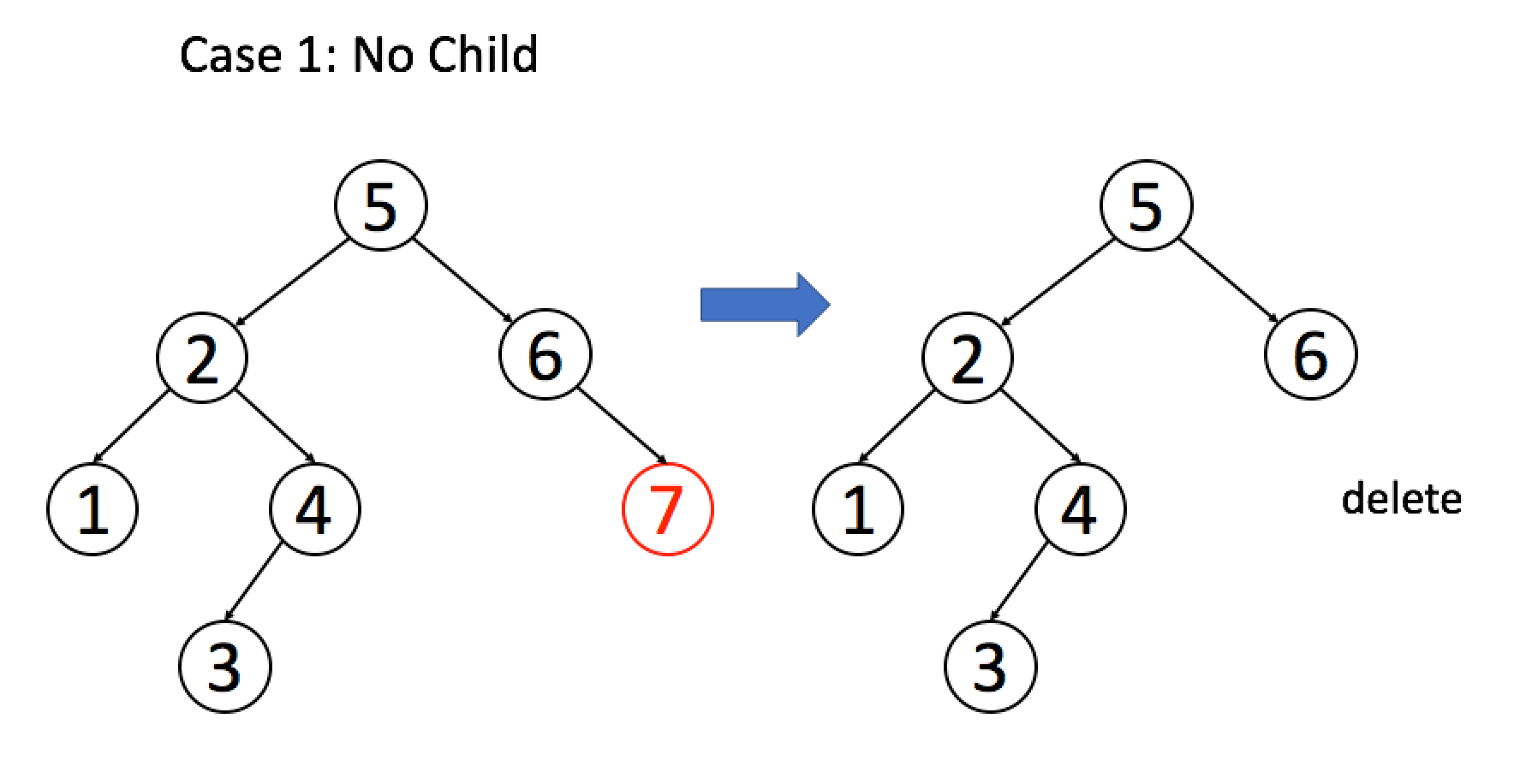
关于如何删除这个节点，有下面的几种情况：

情况一：A这个节点恰好是末端节点，两个子节点为空，那么他就可以当场去世了。

1
2
3
if(!root.left&&!root.right){
    return null;
}

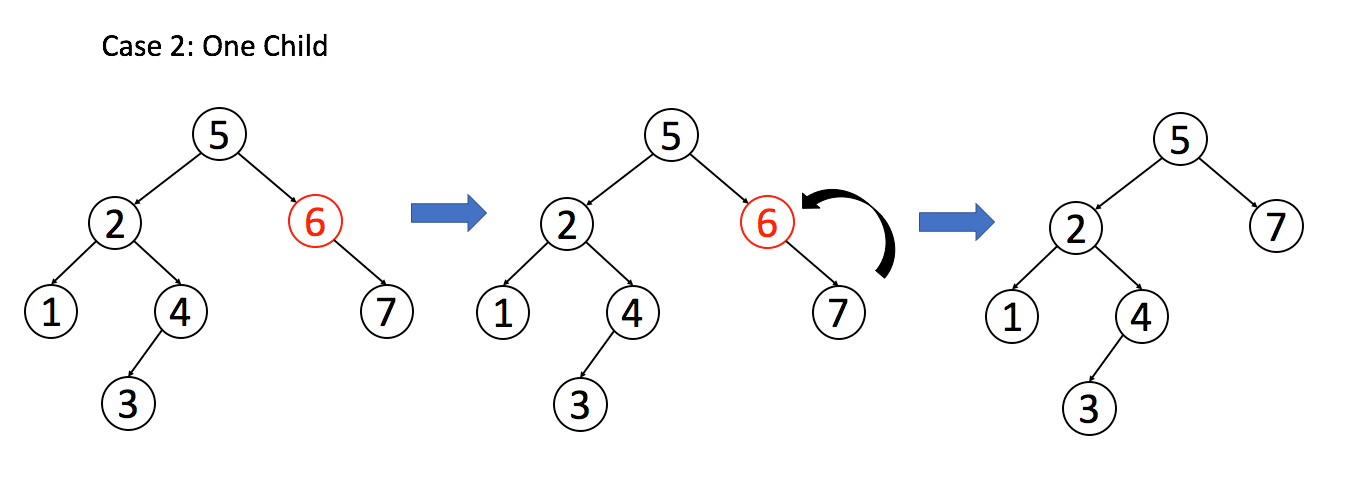
情况二：A只有一个非空字节点，那么就要让这子节点替代自己的位置

1
2
if(!root.left)return root.right;
if(!root.right)return root.left;

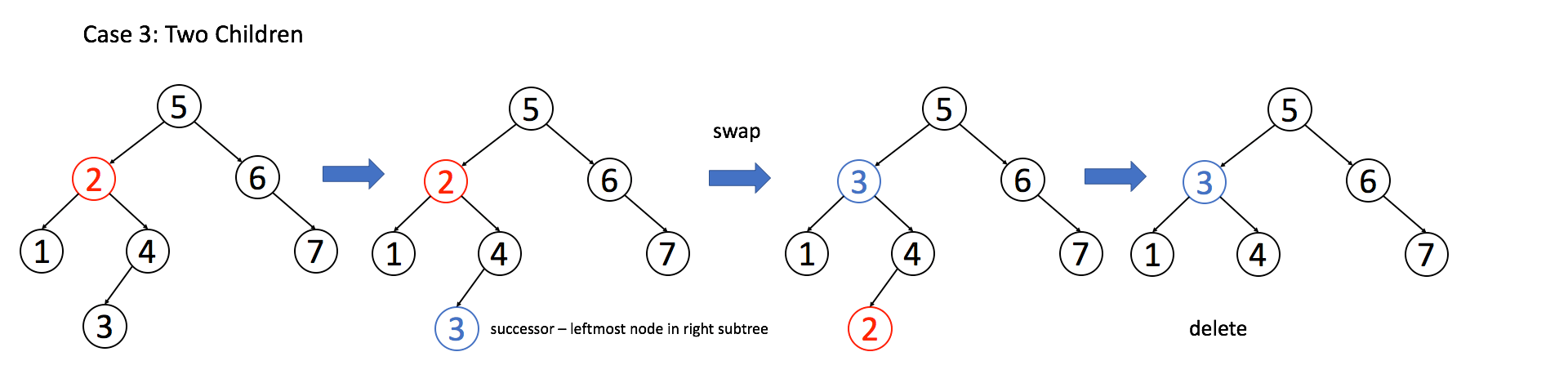
情况三：A有两个子节点，那么就比较复杂了，需要找到右子树最小的节点来替代自己

1
2
3
4
5
6
7
8
if(root.left&&root.right){
    let minNode = getMin(root.right);
    root.val = minNode.val;
    root.right = deleteNode(root.right,minNode.val)
    minNode.left = root.left;
    minNode.right = root.right;
    root = minNode;
}

完整code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
var deleteNode = function (root, key) {
    if(!root) return null;
    if(root.val === key){
        if(!root.left)return root.right;
        if(!root.right)return root.left;
        if(root.left&&root.right){
            let minNode = root.right;
            while(minNode.left){
                minNode = minNode.left;
            }
            root.right = deleteNode(root.right,minNode.val);
            minNode.left = root.left;
            minNode.right = root.right;
            root = minNode
        }
    }else if(root.val < key){
        root.right = deleteNode(root.right,key);
    }else{
        root.left = deleteNode(root.left,key);
    }
    return root;
}

这样就完成了删除的操作，但是有人可能在这一步会好奇，为什么修改root节点这么麻烦，直接修改val值不是更方便吗

1
2
3
4
5
6
7
minNode.left = root.left;
minNode.right = root.right;
root = minNode

=》

root.val = minNode.val;

对于这道题来说是可以这么做的，但是不提倡，因为在实际应用中，BST 节点内部的数据域是用户自定义的，可以非常复杂，而 BST 作为数据结构（一个工具人），其操作应该和内部存储的数据域解耦，所以我们更倾向于使用指针操作来交换节点，根本没必要关心内部数据。

总结

通过这篇文章，我们能学会几个关键的操作，BST的增删改查，和合法性判断。

技巧如下：
根据二叉树的递归得到BST的代码框架

1
2
3
4
5
6
7
8
9
const BST = (n,target)=>{
    if(root.val===target){
        //do something
    }else if(root.val<val){
        BST(root.right,target);
    }else if(root.val>val){
        BST(root.left,target);
    }
}