前言

记录常用排序算法的算法思想和实现，力争基础达标，往后深入的点分开补充~

关键词：常用算法、sort排序、冒泡排序、插入排序、选择排序、快速排序、归并排序、桶排序、希尔排序

sort排序

直接使用api就能进行排序，注意的点是：
不传参，默认是unicode排序，所以常用来排序字母

let str = "asbcascacsac";
let arr = str.split("");
let sortArr = arr.sort();
console.log(sortArr)
/*
[
    'a', 'a', 'a', 'a',
    'b', 'c', 'c', 'c',
    'c', 's', 's', 's'
]
*/

传参，默认两个参，名字无所谓，这里举例是a和b，看返回值来决定升序降序

let arr = [1,5,8,8,4,116516,1213,123]
let arr2 = JSON.parse(JSON.stringify(arr))
let upArr = arr.sort((a,b)=>a-b);
let downArr = arr2.sort((a,b)=>b-a);
console.log(upArr)
console.log(downArr)
/*
[
     1,      4,   5,
     8,      8, 123,
  1213, 116516
]
[
  116516, 1213, 123,
       8,    8,   5,
       4,    1
]
*/

冒泡排序

思想：从第一个元素开始比较相邻的元素大小，大则交换(升序)
时间复杂度：O(n²)

let arr = [1,5,8,8,4,116516,1213,123]
const bubblesort = (arr =>{
    let len = arr.length;
    for(let i=0;i<len-1;i++){
        for(let j=0;j<len-i-1;j++){
            if(arr[j+1]<arr[j]){
                [arr[j],arr[j+1]] = [arr[j+1],arr[j]];
            }
        }
    }
    return arr;
})
console.log(bubblesort(arr))
/*
[
     1,      4,   5,
     8,      8, 123,
  1213, 116516
]
*/

优化：如果原数组已经是排序数组，就不必再排，用flag

const bubblesort = (arr => {
    let len = arr.length;
    for (let i = 0; i < len - 1; i++) {
        let flag = false;
        for (let j = 0; j < len - i - 1; j++) {
            if (arr[j + 1] < arr[j]) {
                [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
                flag=true;
            }
        }
        if(!flag)return arr;
    }
    return arr;
})
console.log(bubblesort(arr))

选择排序

思想：每次都找到最小值放在头部，然后缩小范围继续操作直到完全有序
时间复杂度：O(n²)

const selectsort = (arr => {
    let len = arr.length;
    for (let i = 0; i < len - 1; i++) {
        let minIndex = i;
        for (let j = i; j < len; j++) {
            if(arr[minIndex]>arr[j]){
                minIndex = j;
            }
        }
        if(minIndex!==i){
            [arr[minIndex],arr[i]] = [arr[i],arr[minIndex]];
        }
    }
    return arr;
})
console.log(selectsort(arr))

插入排序

原理：当每次排序的时候，如果前面的元素大于当前的元素，那么将前面的元素转换成当前元素，继续比较，最后替换回最开始转换的元素
时间复杂度：O(n²)
eg

5 3 2 4 1
经过第一轮（单个元素可以当成有序的数列所以忽略第一个元素） 从index1开始保存变量，也就是temp3和5对比
如果3<5，5就在前面腾出一个位置给3'5 5 2 4 1' （arr[j-1]=arr[j]）;
最后还原temp就变成
3 5 2 4 1
第二轮 对比5和2 此时5前面需要腾出一个位置给2(2<5)此时变成'3 5 5 4 1' 然后又发现2<3(j--) 则继续腾位置'3 3 5 4 1'(使用while的原因)最后
2 3 5 4 1
...
1 2 3 4 5

code

function insertSort(arr) {
    for(let i=1;i<arr.length;i++){
        let j=i;
        let temp = arr[i];
        while (j>0&&arr[j-1]>temp) {
            arr[j] = arr[j-1];//arr[1]3->5
            j--;
        }
        arr[j] = temp;//arr[0]5->3
    }
    return arr;
}

归并排序

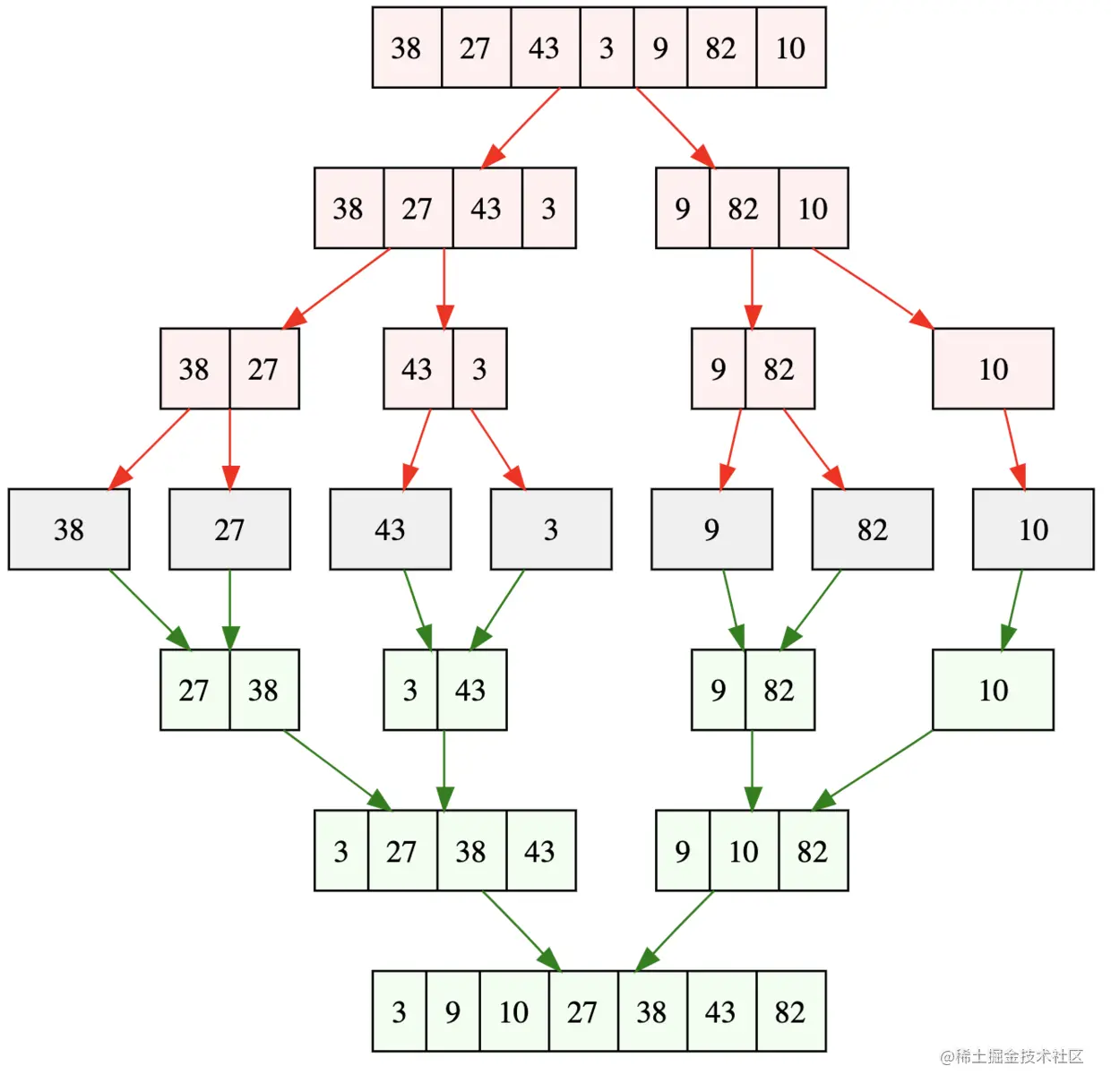
原理：采用分治思想，分解每个子问题，整个数组可以对半分割，一直到分割最小的状态，然后开始逐渐合并，从规模1到规模2一直到还原回整个数组。

时间复杂度：O(nlog(n))

例子：[8, 7, 6, 5, 4, 3, 2, 1];

首先分割，我们利用递归的方法，注意边界小于等于1直接返回arr

1
2
3

[8, 7, 6, 5, | 4, 3, 2, 1]
[8, 7,| 6, 5, | 4, 3, |2, 1]
[8,| 7,| 6, | 5, | 4,|  3, |2,|  1]

此时的规模已经到了最小状态，那么开始两两合并,这里利用数组的push

[7,| 8,| 5, | 6, | 3,|  4, |1,|  2]
[7, 8,| 5, 6, | 3, 4, |1, 2]
[5, 6, 7, 8,  | 1, 2, 3, 4]
[1, 2, 3, 4, 5, 6, 7, 8]

如果已经有一方的合并完全了，那么直接concat另一边剩下的

具体代码

//分解
const mergeSort = arr =>{
    const len = arr.length;
    if(len<2)return arr;
    const mid = len/2,
        left = mergeSort(arr.slice(0,mid)),
        right = mergeSort(arr.slice(mid));
    return mergeArr(left,right);
}
//合并
const mergeArr = (left,right) =>{
    const result = [];
    while(left.length && right.length){
        if(left[0]<=right[0]){
            result.push(left.shift());
        }else{
            result.push(right.shift());
        }
    }
    result.push(...left,...right);
    return result;
}
console.log(mergeSort([4,54,654,12,3,45,1,2]))

归并排序是原地排序吗？

实际上它在合并的时候，借助了额外的空间，但是合并完成之后额外的空间又被释放了。所以不是原地排序

归并排序稳定吗？

merge方法里面的left[0]<=right[0]保证了值相同的元素在合并前后的顺序不变，所以他是一种稳定的排序

时间复杂度

从效率上看，归并排序可算是排序算法中的佼佼者。假设数组长度为 n，那么拆分数组共需 logn 步, 又每步都是一个普通的合并子数组的过程，时间复杂度为 O(n)，故其综合时间复杂度为 O(nlogn)。
最佳情况：T(n) = O(nlogn)。
最差情况：T(n) = O(nlogn)。
平均情况：T(n) = O(nlogn)。

快速排序

原理：

找到一个基准值，一般是数组中间
创建新的左右空数组，分别存放比基准值小的和比基准值大的数据
3，递归上述操作，直到数组长度小于等于1

特点：

快速、常用

缺点：
需要新建两个数组浪费空间资源

var sortArray = function(nums) {
    const len = nums.length;
    if(len<=1)return nums;
    const mid = Math.floor(len/2);
    // 取出基准值
    const midVal = nums.splice(mid,1)[0];
    // 新建左右数组
    const left = [],right = [];
    // splice了 改变了数组大小
    for(let i=0;i<nums.length;i++){
        if(nums[i]<=midVal){
            left.push(nums[i])
        }else{
            right.push(nums[i])
        }
    }
    return sortArray(left).concat(midVal,sortArray(right));
};

快速排序是原地排序吗？

在分区的时候，他不需要很多额外的空间，所以是原地排序操作。

快速排序稳定吗？

和选择排序类似，快速排序可能不是相邻的，因此他有可能打破原来相同元素之间的顺序，所以是不稳定的。

快速排序的时间复杂度

快速排序的时间复杂度是多少？
极端的例子：如果数组中的数据原来已经是有序的了，比如 1，3，5，6，8。如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n / 2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。
最佳情况：T(n) = O(nlogn)。
最差情况：T(n) = O(n2)。
平均情况：T(n) = O(nlogn)。