前言

在上一篇基操篇我们讲述了BST的判断合法性和增删改查，下面来学习BST的构造，读完本文你对下面的题目会有更深入的了解。

Leetcode
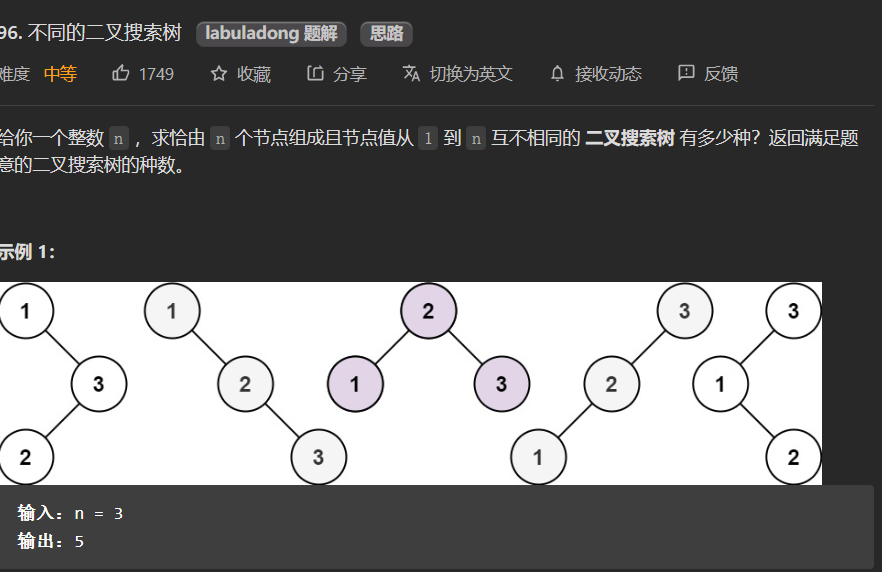
96.不同的二叉搜索树
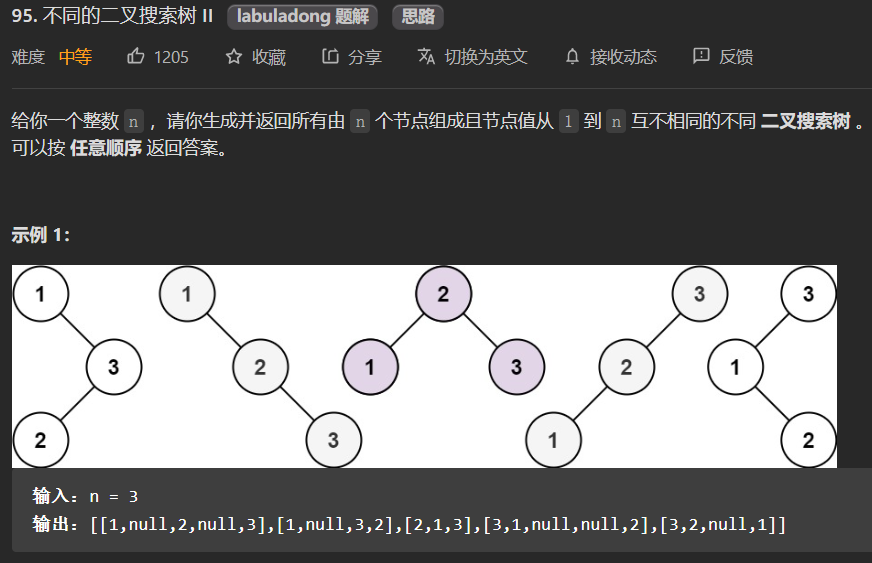
 95.不同的二叉搜索树 II

不同的二叉搜索树

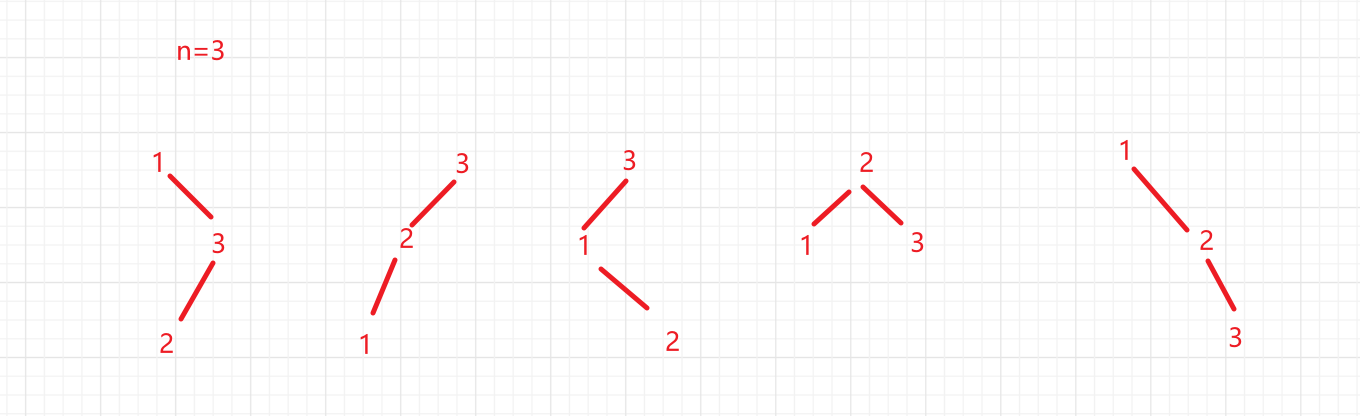
这是一道穷举的题目，首先我们做个例子:比如输入n=3，那么就有以下几个情况

这个是一个正宗的穷举问题，那么有什么方法可以正确的穷举BST的数量呢？

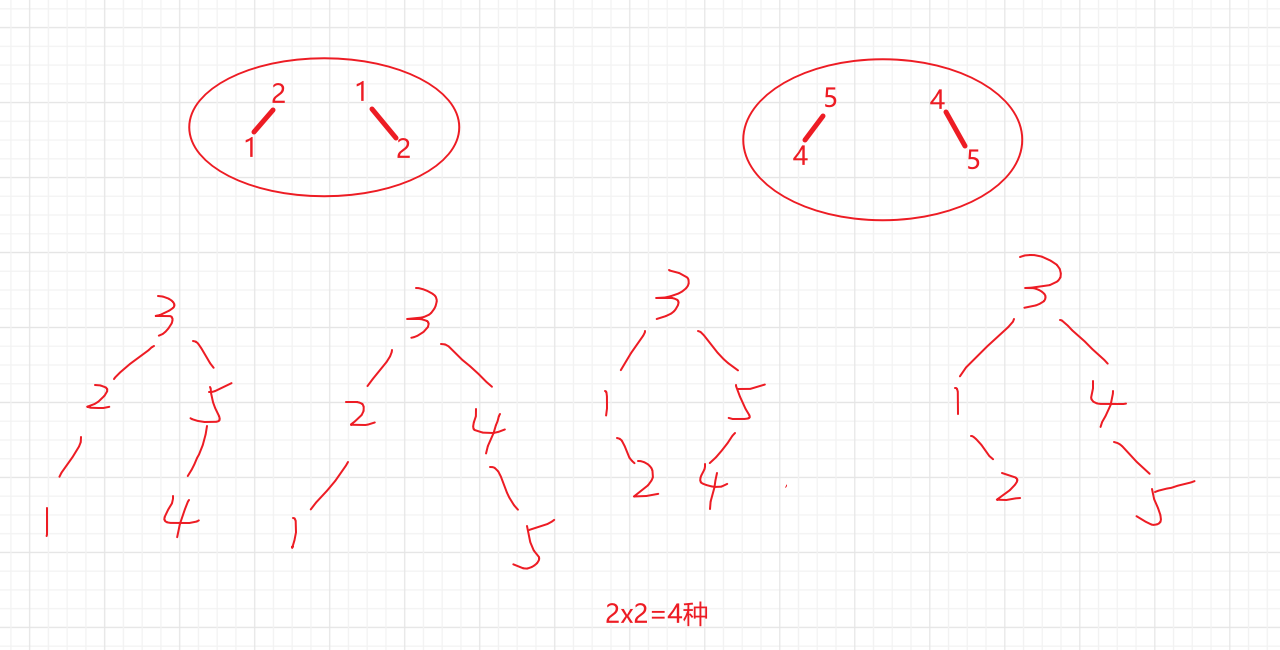
再看一个例子比如给算法输入n=5也就是要求他从1,2,3,4,5里面找数字构成BST

显然会有五种情况，因为每个数字都可以作为根节点，那么我们固定3为根节点，看到底能构成多少个BST

因为BST左小右大的性质，很明显3为根节点的时候，左子树节点就是1,2右子树节点就是4,5

那么左子树的组合数和右子树的组合数的乘积就是3作为根节点的时候的BST个数

在代码方面，其实我们只需要递归就可以了

// 计算闭区间[1,n]组成的BST数量
const numTree = n=>{
  return count(1,n);
  const count = (start,end)=>{
      // base case
      if(start>end)return 1;
      let res = 0;
      for(let i=start;i<=end;i++){
          let left = count(start,i-1);
          let right = count(i+1,end);
          res += left*right;
      }
      return res;
  }
}

但是这样做显然是不行的，因为会存在很多重叠子问题，我们可以利用一个memo备忘录来解决这个问题

var numTrees = function(n) {
    const memo = new Map();
    const count = (lo,hi)=>{
        // base case
        if(lo>hi)return 1;
        let memoKey = `${lo}&${hi}`;
        if(memo.has(memoKey)){
          return memo.get(memoKey)
        }
        let res = 0;
        for(let mid = lo;mid<=hi;mid++){
          let left = count(lo,mid-1);
          let right = count(mid+1,hi);
          res += left*right;
        }
        memo.set(memoKey,res);
        return res;
    }
    return count(1,n);
}

不同的二叉搜索树II

题目类似，但是最后要返回全部组合的BST

我们不难想到还是要用memo去记录我们的子问题，并且这里还存在一个关键，就是我们可以用简单的memoKey来帮助我们记录

var generateTrees = function(n) {
    if(n===0)return [];
    const memo = new Map();

    const count = (lo,hi)=>{
        let res = [];
        // base case
        if(lo>hi){
            res.push(null);
            return res;
        }
        //定义memoKey
        let memoKey = `${lo}&${hi}`;
        //查找备忘录
        if(memo.has(memoKey)){
            return memo.get(memoKey);
        }
        // 穷举root节点的所有BST可能
        for(let i=lo;i<=hi;i++){
            // i作为根节点
            let leftTree = count(lo,i-1);
            let rightTree = count(i+1,hi);
            // 穷举root的所有左右子树组合
            for (const left of leftTree) {
                for (const right of rightTree) {
                    res.push(new TreeNode(i,left,right))
                }
            }
        }
        //存放res
        memo.set(memoKey,res);
        return res;
    }
    return count(1,n);
}