前言

在前面的文章我们学习了寻找一颗二叉树的重复子树，这个问题结合了第四章节的序列化内容加第三章节的构造内容，接下来我们学习二叉搜索树的知识，读完本文你对以下的题目有更深刻的了解：

Leetcode
230.二叉树中的第k小元素
 538.把二叉搜索树转为累加树
 1038.把二叉搜索树转为累加树

Binary Search Tree

全称二叉搜索树，简写BST，特性如下：

BST的每个节点，左子树节点的值都比他小，右子树节点的值都比他大。
对于BST的每一个节点，他的左侧子树和右侧子树都是BST

labuladong原话：二叉搜索树并不算复杂，但我觉得它可以算是数据结构领域的半壁江山，直接基于 BST 的数据结构有 AVL 树，红黑树等等，拥有了自平衡性质，可以提供 logN 级别的增删查改效率；还有 B+ 树，线段树等结构都是基于 BST 的思想来设计的。

从算法题的角度来讲，中序遍历一个BST，是升序的，因为他先构造了左子树再构造右子树，所以如果是以一个数组的形式显示，就是从小到大的。

寻找第 K 小的元素

按照上面的思路，我们只要中序遍历这个二叉树然后找第k个就行了

var kthSmallest = function(root, k) {
    let res;
    const inorder = root =>{
        if(!root)return;
        inorder(root.left);
        k--;
        if(k===0)res = root.val;
        inorder(root.right);
    }
    inorder(root);
    return res;
};

虽然这道题做完了，但是这个解法在目前来说并不是最高效的。下面引自labuladong

如果按照我们刚才说的方法，利用「BST 中序遍历就是升序排序结果」这个性质，每次寻找第 k 小的元素都要中序遍历一次，最坏的时间复杂度是 O(N)，N 是 BST 的节点个数。

要知道 BST 性质是非常牛逼的，像红黑树这种改良的自平衡 BST，增删查改都是 O(logN) 的复杂度，让你算一个第 k 小元素，时间复杂度竟然要 O(N)，有点低效了。

所以说，计算第 k 小元素，最好的算法肯定也是对数级别的复杂度，不过这个依赖于 BST 节点记录的信息有多少。

我们想一下 BST 的操作为什么这么高效？就拿搜索某一个元素来说，BST 能够在对数时间找到该元素的根本原因还是在 BST 的定义里，左子树小右子树大嘛，所以每个节点都可以通过对比自身的值判断去左子树还是右子树搜索目标值，从而避免了全树遍历，达到对数级复杂度。

那么回到这个问题，想找到第 k 小的元素，或者说找到排名为 k 的元素，如果想达到对数级复杂度，关键也在于每个节点得知道他自己排第几。

比如说你让我查找排名为 k 的元素，当前节点知道自己排名第 m，那么我可以比较 m 和 k 的大小：

1、如果 m == k，显然就是找到了第 k 个元素，返回当前节点就行了。

2、如果 k < m，那说明排名第 k 的元素在左子树，所以可以去左子树搜索第 k 个元素。

3、如果 k > m，那说明排名第 k 的元素在右子树，所以可以去右子树搜索第 k - m - 1 个元素。

这样就可以将时间复杂度降到 O(logN) 了。

那么，如何让每一个节点知道自己的排名呢？

这就是我们之前说的，需要在二叉树节点中维护额外信息。每个节点需要记录，以自己为根的这棵二叉树有多少个节点。

也就是说，我们 TreeNode 中的字段应该如下：

class TreeNode {
    int val;
    // 以该节点为根的树的节点总数
    int size;
    TreeNode left;
    TreeNode right;
}

有了 size 字段，外加 BST 节点左小右大的性质，对于每个节点 node 就可以通过 node.left 推导出 node 的排名，从而做到我们刚才说到的对数级算法。

当然，size 字段需要在增删元素的时候需要被正确维护，力扣提供的 TreeNode 是没有 size 这个字段的，所以我们这道题就只能利用 BST 中序遍历的特性实现了，但是我们上面说到的优化思路是 BST 的常见操作，还是有必要理解的。

BST转累加树

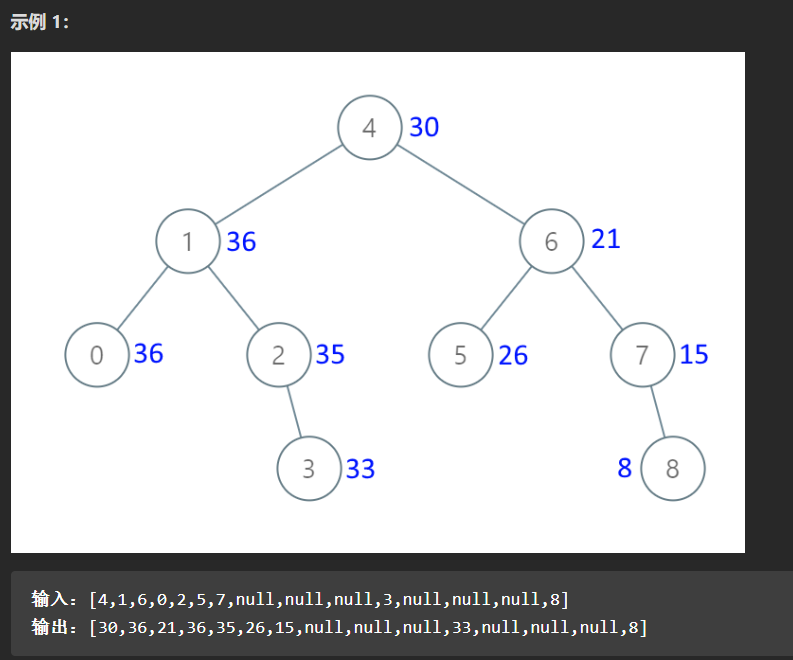
力扣538和1038题都是这一道，可以一起做了。

按照二叉树的通用思路，我们要思考每个节点本身应该做什么，但是这道题很难想到什么思路。

但是我们可以这样想，我们的目的是什么，是将节点进行一个累加然后赋值到这个节点，中序遍历的性质就是能将BST变成升序。

不过一般的中序可做不到这个特点，因为是左根右，只能打印出升序的，我们现在需要从右子树开始计算，所以可以使用右根左，打印出降序的。

var convertBST = function (root) {
  let sum = 0;
  const inorder = n=>{
    if(!n)return null;
    inorder(n.right);
    sum+=n.val;
    n.val = sum;
    inorder(n.left);
    return n
  }
  return inorder(root);
}