前言

在上一篇手把手二叉树的笔记中，我们解决了三道问题，二叉树最大深度，二叉树最大直径，和层序遍历。而读完本文，你可以解决以下问题：

Leetcode
226.翻转二叉树
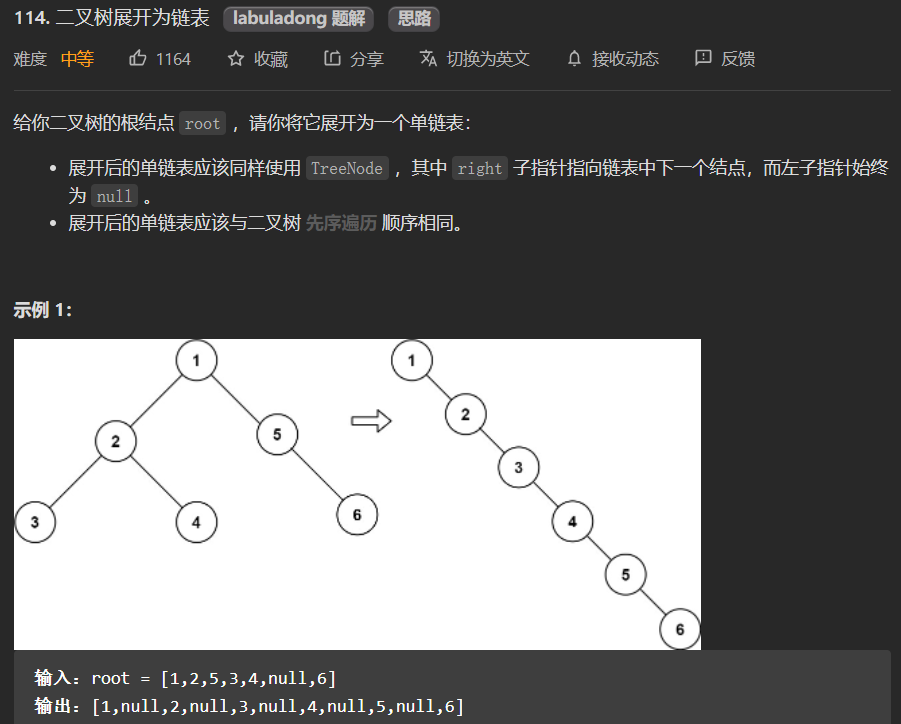
114.将二叉树展开为链表
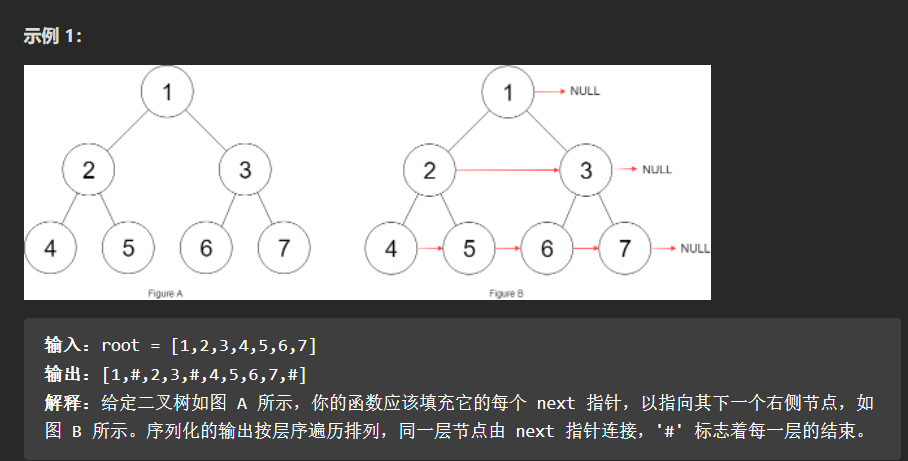
116.填充二叉树节点的右侧指针

再谈二叉树的重要性

对于经典的算法快速排序和归并排序来说，如果你知道二叉树的前序遍历就是快速排序，后序遍历就是归并排序，那么你对二叉树就有比较深入的了解了。

快速排序的逻辑是先找到一个基准点，根据这个基准点，去对我们左侧的数据划分，使得左侧的数据都小于这个基准点，右侧的数据都大于这个基准点，然后在左侧和右侧进行递归这个过程，最后的数组就是被排序的

代码逻辑过程：

const quickSort = (arr,i,j)=>{
    let p = Math.floor(arr.length/2);
    ...
    quickSort(arr,i,p-1);
    quickSort(arr,p+1,j);
    ...
}

先构造分界点，再根据左右子数组去构造分界点，这不就是二叉树的前序遍历吗

再谈谈归并排序的逻辑，先分割数组，到最小规模后逐步合并子数组，直到完全有序

代码逻辑过程：

const mergeSort = (arr)=>{
    let mid = Math.floor(len/2);
    //分割
    left = mergeSort(arr.slice(0,mid));
    right = mergeSort(arr.slice(mid,len));
    ···
    //合并
    arr = mergeArr(left,right);
}

是不是发现了他很像后序遍历，先对左右数组排序然后合并。

所以接下来做几道比较有意思的二叉树算法题

递归的诀窍

写递归算法的诀窍就是明确函数定义的是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要试图跳入递归。

用个具体的例子来解释：求一颗二叉树有多少节点

const count = (n)=>{
    if(!n)return 0;
    return 1 + count(n.left) + count(n.right);
}

这个例子非常简单，用根节点加左右子树的节点就是总节点。那左右子树的节点怎么计算？就是调用递归的count计算出来的。

写树相关的算法，简单来说就是搞清楚当前root节点要做什么，然后根据函数定义递归子节点，递归调用会让孩子做相同的事情。

实操

题目一：翻转二叉树-226

     4
   /   \
  2     7
 / \   / \
1   3 6   9

=>

     4
   /   \
  7     2
 / \   / \
9   6 3   1

我们发现只要将二叉树的左右节点都交换就可以完成这个过程。

//后序
var invertTree = function(root) {
    if(!root)return root;
    invertTree(root.left);
    invertTree(root.right);
    [root.left,root.right] = [root.right,root.left];
    return root;
};
//前序
var invertTree = function(root) {
    if(!root)return null;
    [root.left,root.right] = [root.right,root.left];
    invertTree(root.left);
    invertTree(root.right);
    return root;
};

这道题你会发现前序和后序都能做，但是中序就不行。因为中序的遍历是一边先结束再另一边，所以做不到反转。边界条件的话，因为前序可能是一开始就无，所以是null，而后序最后是根，所以是root

题目二：填充二叉树节点的右侧指针-116

我们仿造上面的思路其实可以这样做

var connect = function(root) {
    if(!root||!root.left)return root;
    root.left.next = root.right;
    connect(root.left);
    connect(root.right);
    return root
}

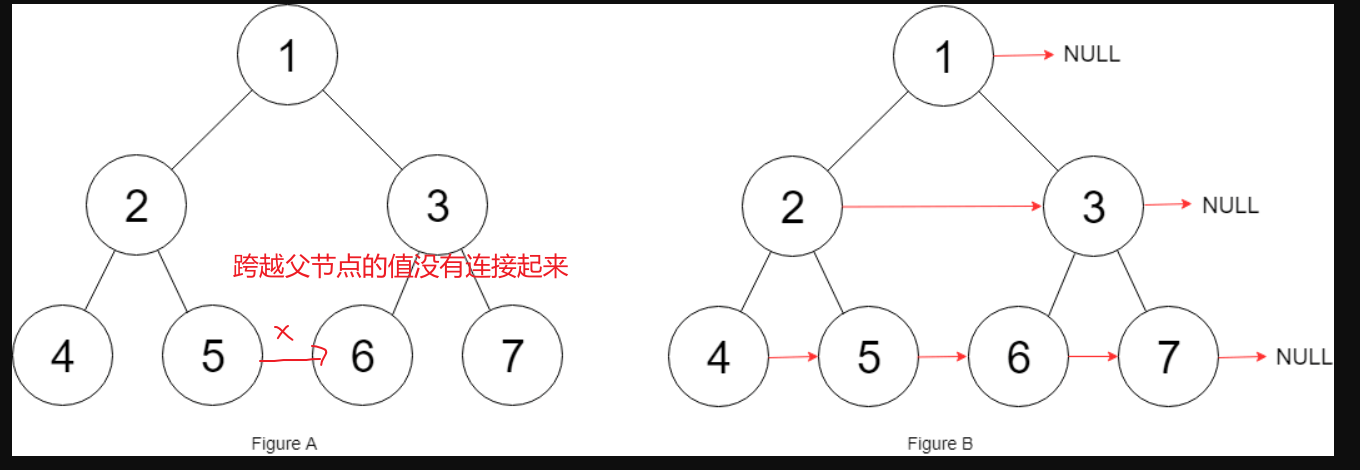
不过这样其实有很大的问题

我们发现跨越父节点的值并没有被连接起来。

稍微改造一下代码

var connect = function(root) {
    if(!root)return null;
    const connectTwo = (n1,n2)=>{
        //其中一者没有直接返回上一步
        if(!n1||!n2)return;
        n1.next = n2;
        // 相同父节点的左右连接
        connectTwo(n1.left,n1.right);
        connectTwo(n2.left,n2.right);
        // 跨越父节点的左右连接
        connectTwo(n1.right,n2.left);
    }
    connectTwo(root.left,root.right);
    return root;
}

这样使用connectTwo递归就可以无死角的覆盖整颗二叉树，将所有相邻的节点连接起来了。

题目三：将二叉树展开为链表-114

那么我们要怎么做才能拉平这个数组呢？

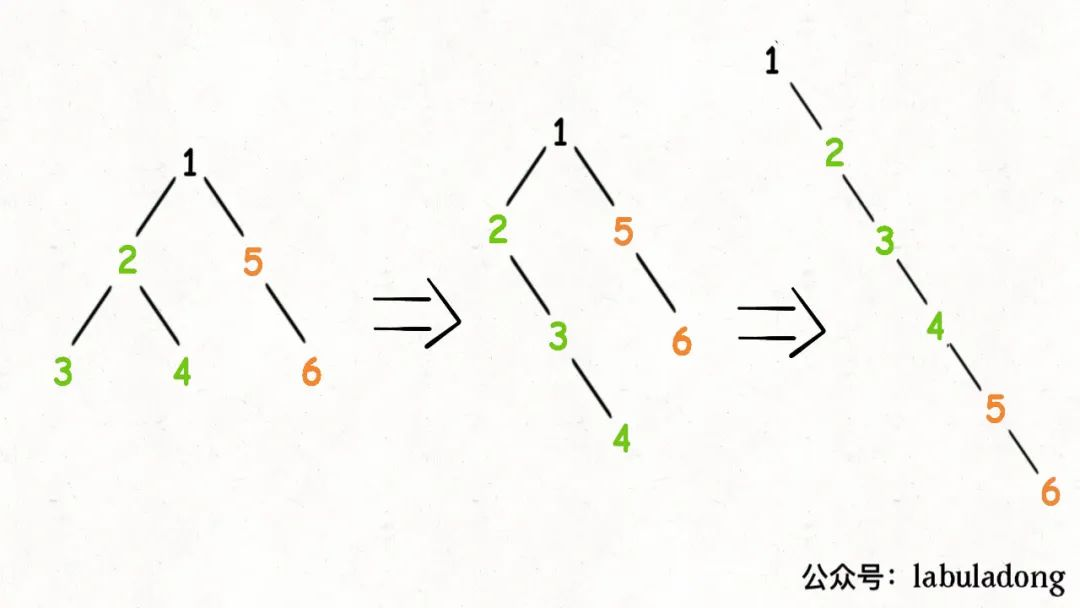
可以看出，我们首先需要将左子树拉平，然后将右子树拉平，然后再把左子树接到右子树上。

那么就第一步怎么拉平左右子树呢？

我们根据后序遍历动画可以知道，只要经过后序遍历，就能拉平左右子树，那么第一步的问题就解决了。

随后是怎么把左子树接到右子树上面呢？

首先我们要清楚，这个左子树不是中途就能插入的，我们必须先把左右子树保存，然后删掉左子树，将保存的左子树放到右子树，再将保存的右子树插入到右子树。

var flatten = function(root) {
    if(!root)return;
    //拉平
    flatten(root.left);
    flatten(root.right);
    //暂存左右子树
    let left = root.left;
    let right = root.right;
    //删除原左子树，将暂存的左子树放在原右子树上
    root.left = null;
    root.right = left;
    //类似于链表 遍历右子树找到他末尾节点 然后插入暂存右子树
    let p = root;
    while(p.right!==null){
        p = p.right;
    }
    p.right = right;
}