前言

labuladong的二叉树算法入门第一章，这段时间的算法确实没什么长进，只停留在会做针对性的题目的阶段，如果出现了变体就很难解决了，所以下决心从算法基础再开始修炼算法。由于labuladong的代码大多数是c++，本文便修改为js进行学习。

读完本文，你可以解决以下问题：
104.二叉树的最大深度
543.二叉树的直径
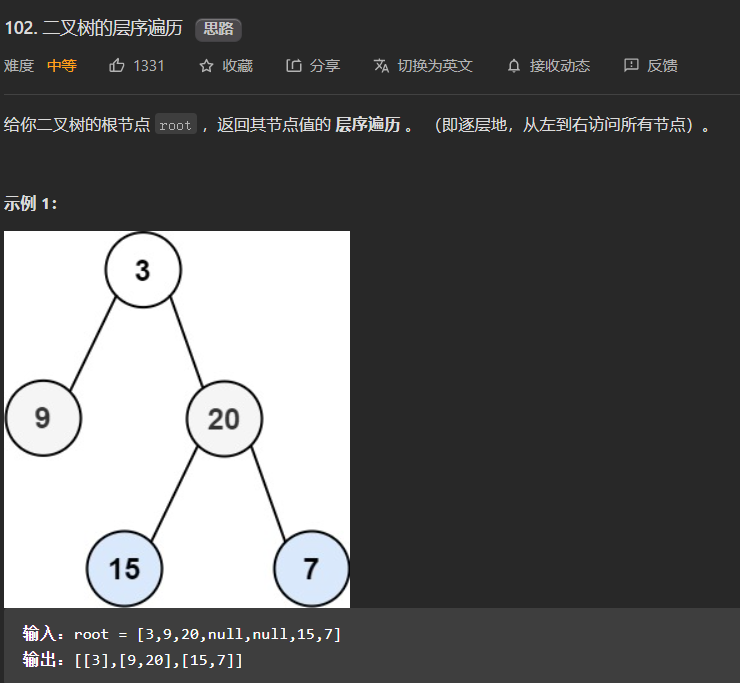
102.二叉树的层序遍历

二叉树学习的必要性

二叉树是所有高级算法的基础，他涉及了递归，回溯，所以算法入门最好就从二叉树开始。

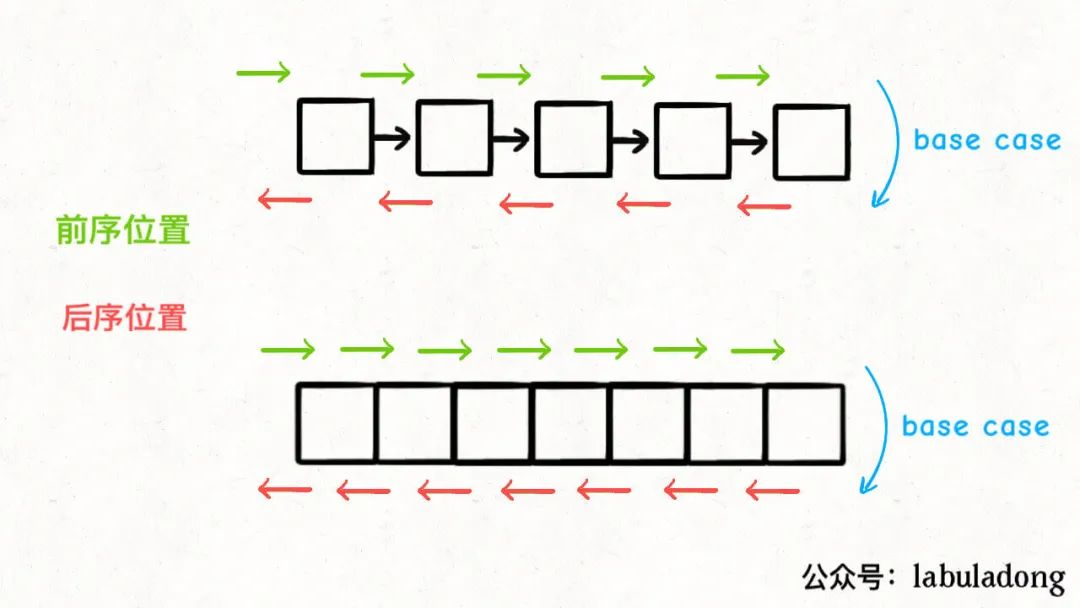
深入理解前中后序

根左右，左根右，左右根…可能很多人在学习数据结构的时候，老师教过这样的判断过程。这三句话对应着二叉树的前中后序，但实际上你真的理解这三种遍历顺序吗

从前序开始看，我们知道，有这样的代码

if(!root)return;
console.log(root);
traverse(root.left);
traverse(root.right);

其实这个就是一个一次遍历，和遍历数组链表的方式大同小异，而所谓的前序遍历，只不过进入第一个节点就开始遍历，而后序遍历是离开一个节点的时候才开始遍历,中序遍历是在遍历完左子树，即将遍历右子树的时候才执行。

这之中利用到了递归和回溯的这个特性，我们规定了遍历到最后才返回的时机，就能实现后序遍历，

解题的思路

二叉树题目的递归解法可以分为两类，一类是一次遍历实现的结果，第二类是分解问题得到答案，这两类思路分别对应着回溯算法核心框架和动态规划核心框架

在leetcode第104题中，求二叉树的最大深度，这道题很明显，思路就是遍历一次二叉树，记录每个节点的深度，取叶子节点深度的最大值即可，这就是一次遍历完成的结果。

var maxDepth = function (root) {
    let max = 0;
    let depth = 0;
    if (!root) return 0;
    const deep = (n) => {
        if (!n) {
            max = Math.max(max, depth);
            return;
        }
        depth++;
        deep(n.left);
        deep(n.right);
        depth--;
    }
    deep(root);
    return max;
};

这道题无关遍历的顺序，有关系的只是什么时机去刷新这个max。并且我们知道前序的条件是进入一个节点之前，所以我们使用了depth++，后序是在离开一个节点的时候，所以depth—，这个depth记录了当前递归的节点深度，所以要这样维护他。

除此之外，我们也很容易知道，二叉树的最大高度可以通过子树的最大高度计算出来，这就是分解问题的关键。

var maxDepth = function (root) {
    const deep = (n,l)=>{
        if(!n){
            return 0;
        }
        let left = deep(n.left,l+1);
        let right = deep(n.right,l+1);
        let max = Math.max(left,right)+1;
        return max;
    }
    return deep(root,0);
};

这个思路的核心在于，要使用递归先获得子树的最大高度，那么要获得这个最大高度，就需要遍历完这个子树，这个时候，代码逻辑写在后序的部分就显得尤为重要，因为此时一个完整的子树已经被遍历了，我们只需要在这个阶段获取最大高度刷新即可。

后序的特殊之处

我们知道前序是刚刚进入节点的时刻，后序是即将离开节点的时刻，前序自顶向下，后序自底向上。那么就意味着，前序的代码只能获取父节点传递过来的数据。后序的代码不仅可以获取数据，还能拿到子树通过函数返回的数据

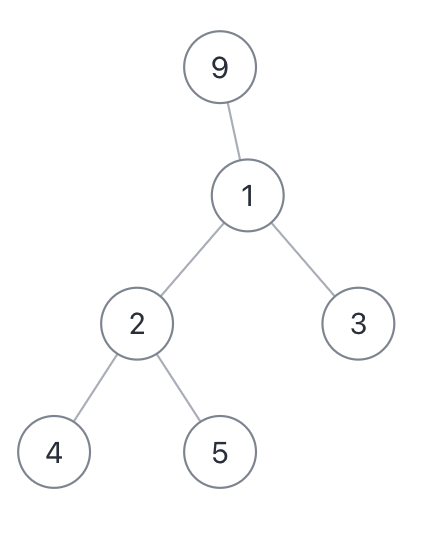
举个例子，现有一颗二叉树，处理以下两个问题：

如果把根节点看成第一层，如何知道每个节点的层数
如何打印每个节点的左右子树有多少个节点？并返回节点总数

首先第一个代码

var traverse = (root,level)=>{
    if(!root)return;
    console.log(root,level);
    traverse(root.left,level+1);
    traverse(root.right,level+1);
}
traverse(root,1);

第二个代码

var traverse = (root,level)=>{
    if(!root)return 0;
    let left = traverse(root.left,level+1);
    let right = traverse(root.right,level+1);
    console.log(root,left,right);
    return left+right+1;
}

因此我们发现，只有后序才能够帮助我们获取子树的信息，所以一旦发现题目和子树有关，大概率代码的位置要写在后序的部分。

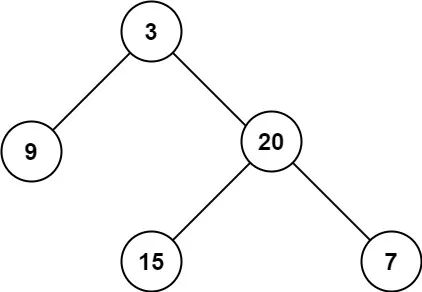
那么后序在二叉树刷题中是如何发挥作用的，这里看一道leetcode的543题，二叉树直径，计算出二叉树直径的最大长度。

所谓的二叉树的直径，就是两个任意节点之间的路径长度。最大路径长度不一定是要穿过根节点，看下图

这个图片中，最大的路径长度有两条，1是[4,2,1,3],2是[5,2,1,3]

这道题的关键在于，每一条二叉树的直径就是一个节点的左右子树最大深度之和，比如说这个节点1 左子树最大深度2，右子树最大深度1 加起来就是3

var diameterOfBinaryTree = function (root) {
    let max = 0;
    const deep = (n,l)=>{
        if(!n)return 0;//注意深度问题边界是0
        let left = deep(n.left,l+1);
        let right = deep(n.right,l+1);
        max = Math.max(left+right,max);//刷新最大深度之和,这步才是重点
        return Math.max(left,right)+1;//返回最大深度+1；让下一次递归知道长度
    }
    deep(root,0);
    return max;
}

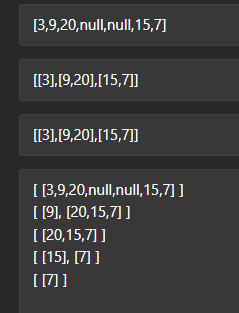
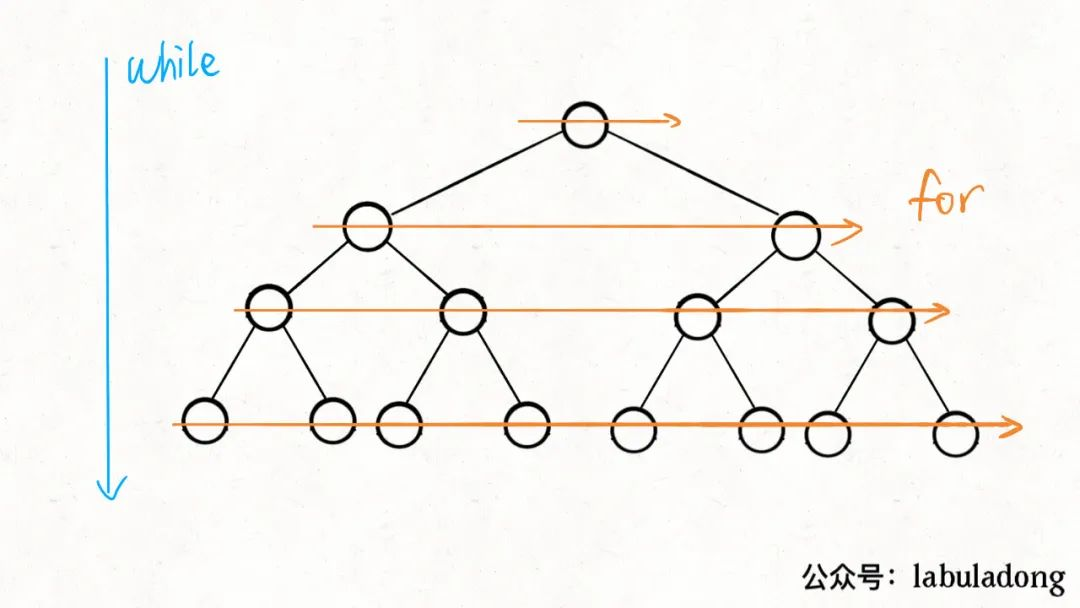
层序遍历

层序便利的思路是使用队列。代码框架如下；

code

var levelOrder = function (root) {
    if (!root) return [];
    const q = [root];
    const res = [];
    while (q.length) {
        let len = q.length
        const temp = [];
        for (let i = 0; i < len; i++) {
            const n = q.shift();
            temp.push(n.val);
            if (n.left) q.push(n.left);
            if (n.right) q.push(n.right);
        }
        res.push(temp);
    }
    return res;
};